等比数列的基本运算
共112题

· 等比数列的基本运算

等比数列的基本运算
共112题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知等比数列的公比，且．

16.求的值；

17.若，求数列的前项和．

第(1)小题正确答案及相关解析

正确答案

解析

【解析】

由题意，得，

或

考查方向

本题主要考查了等比数列的通项公式和等比数列的求和公式，同时也考查了考生的推理论证与运算求解能力。

解题思路

解题步骤如下：1、根据等比数列的通项公式化简等式，即可得到公比的值；2、因为，即可求出首项，易得数列的通项公式，从而求出数列的前项和。

易错点

本题在求等比数列的公比或求数列的前项和时容易发生错误。

第(2)小题正确答案及相关解析

正确答案

解析

【解析】 .

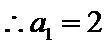
考查方向

本题主要考查了等比数列的通项公式和等比数列的求和公式，同时也考查了考生的推理论证与运算求解能力。

解题思路

解题步骤如下：1、根据等比数列的通项公式化简等式，即可得到公比的值；2、因为，即可求出首项，易得数列的通项公式，从而求出数列的前项和。

易错点

本题在求等比数列的公比或求数列的前项和时容易发生错误。

题型：简答题

简答题 · 12 分

已知是公比不等于1的等比数列，为数列的前项和，且

19.求数列的通项公式；

20.设，若，求数列的前项和．

第(1)小题正确答案及相关解析

正确答案

an=3或

解析

(Ⅰ)设数列{an}的公比为q，

当时，符合条件，，an=3

当时，所以，解得 ----5分

综上：an=3或

考查方向

本题考查了等比数列与等差数列的应用，同时考查了对数运算的应用及裂项求和法的应用．

解题思路

设数列{an}的公比为q，根据公比和进行求解，当时，根据，解出首项和公比，进而求出通项公式.

易错点

容易忽略对这种情况.

第(2)小题正确答案及相关解析

正确答案

解析

证明：若an=3，则bn=0，与题意不符；

，

考查方向

本题考查了等比数列与等差数列的应用，同时考查了对数运算的应用及裂项求和法的应用．

解题思路

化简，从而可得,从而得证．

易错点

对于这种通项公式，求和一般用裂项法，要熟练掌握这种类型题的方法.

题型：单选题

单选题 · 5 分

5.数列满足：（，且），若数列是等比数列，则的值等于（）

正确答案

解析

根据题意可知，由得到

由于数列是等比数列，所以所以选D

考查方向

等比数列的性质

解题思路

根据所给条件化简，求得数列的通项公式，进而求出参数的值

易错点

化简错误，计算能力弱

知识点

等比数列的基本运算

题型：单选题

单选题 · 5 分

4.等比数列｛an｝满足a1=3， =21，则（）

A21

B42

C63

D84

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算

题型：简答题

简答题 · 7 分

21. 正数数列、满足：，且对一切，，是与的等

差中项，是与的等比中项；

（1）若，，求、的值；

（2）求证：是等差数列的充要条件是为常数数列；

充分性和必要性的证明。

（3）记，当，，指出与的大小关系并说明理由；

正确答案

是等差数列的充要条件是为常数数列

解析

正整数数列、满足：，且对一切，，是与的等差中项，是与的等比中项；所以2=+，，，，可得，解得。

是等差数列，，可得，则，

所以时，，

即，正整数数列，可知，，所以，所以数列

为常数数列。是等差数列的充要条件是为常数数列。

对一切，，是与的等

差中项，是与的等比中项；,所以，=，由所以，依此类推可得：为正整数。当，，时

考查方向

数列的综合应用。

解题思路

根据对一切，，是与的等差中项，是与的等比中项；所以2=+，，，，可得即可求解。

是等差数列，，可得，，，，时，，可得即可证明。

对一切，，是与的等差中项，是与的等比中项；，利用基本不等式的性质

可得，，利用单调性即可得出。

易错点

计算要仔细准确。

①不容易考虑到基本不等式②利用单调性比较大小在数列中的应用。

知识点

充要条件的判定等差数列的判断与证明等比数列的基本运算数列与不等式的综合

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 等比数列的判断与证明

百度题库 > 高考 > 理科数学 > 等比数列的基本运算

扫码查看完整答案与解析