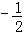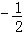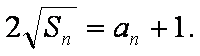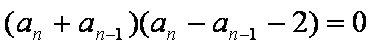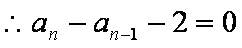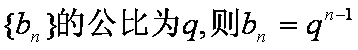- 等比数列的基本运算
- 共112题
数列


(1)求数列
(2)证明:
(3)证明:
正确答案
见解析
解析
解析:(1)解:由

下面用数学归纳法证明猜想:
① 当

② 假设




综合①② 知:猜想成立.即数列的通项公式为
(2)由于当

所以令


∴ 

从而 

(3) 由柯西不等式得:
所以要证
即证 

即证:
因为函数









知识点
等比数列{an}中,a3=6,前三项和S3=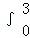
正确答案
1或
解析
S3=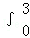
∵a3=6,S3=18
∴a1q2=6,a1+a1q+6=18
∴2q2﹣q﹣1=0解得q=1或
知识点
已知数列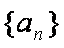
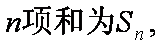
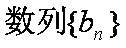
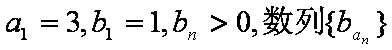
(1)求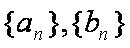
(2)求证:
正确答案
见解析
解析
解析:(1)依题意有: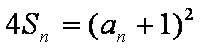
所以当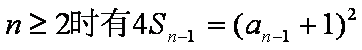
①-②得: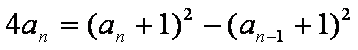
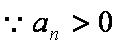
所以数列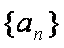
故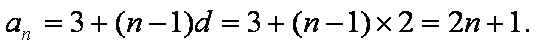
设
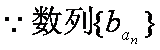
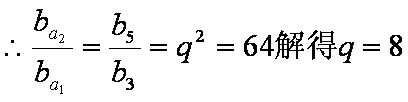
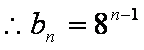
(2)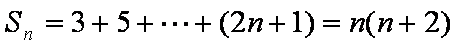
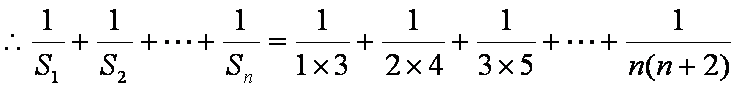
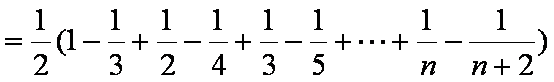
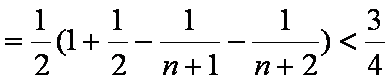
知识点
在等比数列






(1)求
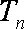
(2)若对任意的


正确答案
见解析。
解析
(1)设



∴
∴
-------------------------------------5分
(2)①当


即
而

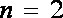

∴
②当


即
而

∴
综上,实数

知识点
已知
(1)求证:数列
(2)求证:
正确答案
见解析。
解析
证明:(1)因为


所以,



因为






数列{ lg(


(2)证明:由(1)知,lg(






因为0<



当n=1,2时,有



所以

所以,
知识点
扫码查看完整答案与解析