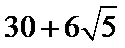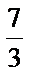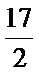- 简单空间图形的三视图
- 共140题
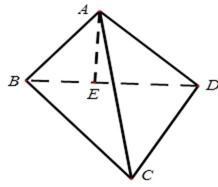
16.多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形
(1)求多面体ABCDEF的体积;
(2)求二面角A-BF-C的余弦值.
正确答案
(1)
(2)
解析
本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)分别取AB、CD的中点M、N,连接EM、EN、MN,多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。由三视图可知,AD=2,AM=DN=1,面ADE为正三角形且垂直于底面ABCD,知F点到底面的距离为



(2)取MN的中点O,BC的中点P,以OM为x轴,OP为y轴,OF为z轴建立坐标系,易知A(1,-1,0),B(1,1,0),F(0,0, 






考查方向
本题考查了立体几何中的体积和二面角的问题.属于高考中的高频考点。
解题思路
无
易错点
1、第一问中的多面体的拆分。
2、第二问中二面角的求解时要建立适当的空间直角坐标系。
知识点
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
该三视图所对应得空间几何体如图所示:根据台体的体积计算公式
考查方向
解题思路
1、首先根据三视图还原出原来的几何体;
2、根据空间几何体的体积计算公式选择合适的公式计算。
易错点
不能根据三视图准确地还原出原来的空间几何体而导致本题不会做。
知识点
11. 如图,是某多面体的三视图,则该多面体的体积为( )
正确答案
解析
由三视图判断知此为四棱锥
如图所示,
故
故选B选项。
考查方向
本题主要考查了由三视图还原成实物图再进行体积与表面积的计算,在近几年的各省高考题出现的频率较高,常是独立命题,求体积、表面积与棱长,也与函数结合求最值问题。
解题思路
由三视图先还原出实物的直观图(可借用正方体),再用相关公式进行求解。
易错点
1、无法由三视图还原出实物直观图。
2、公式不熟悉导致出错。
知识点
10.已知一个几何体的三视图如右图所示,则该几何体的体积为( )
正确答案
解析
根据几何体的三视图,可知,立体图形是以高为2,底面积为2的两个集合组合体,根据几何体的体积公式利用底面积乘以高求得,所以选D
考查方向
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高,三棱锥的高是由垂直与底面的侧面的高得到,本题是一个基础题.
知识点
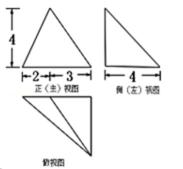
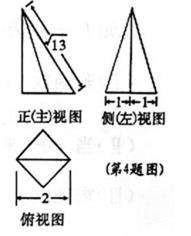
10.某三棱锥的三视图如图所示,该三棱锥的表面积是____________.
正确答案
解析
因为三棱锥的表面积是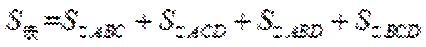
由题意易知
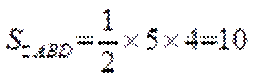
又因为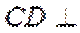
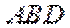
所以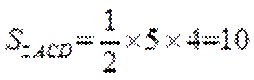
又因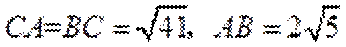
所以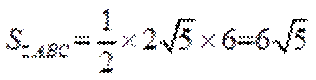
故
考查方向
解题思路
根据主视图和左视图判断俯视图的相关线段的大小
易错点
从三视图还原成空间几何体错误
知识点
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
易知,由该几何体的三视图还原后得到原图如下:依题意知该台体ABC-A1B1C1的表面积为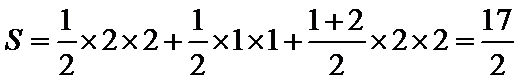
考查方向
解题思路
以三视图为载体考查空间线面位置关系的证明、求解其中一个视图的面积问题、求解几何体的表面积和体积问题等,解决此类问题的关键是能够对给出的三视图进行恰当的分析,从三视图中发现相应的位置关系与数量关系,然后在直观图中解决问.
易错点
不能由三视图还原为原图导致出错。
知识点
5.某三棱锥的三视图如图所示,则该三棱锥四个面的面积中最大的是
正确答案
解析
根据三视图将几何体放到长方体中得到原来几何体为三棱锥








考查方向
解题思路
1、将几何体放到长方体中考虑;
2、得到原来的几何体后计算各个面的面积后选出面积的最大值。
易错点
无法由三视图还原到原来的几何体;
知识点
13. 右图是一个空间几何体的三视图(俯视图外框为正方形),则这个几何体的表面积为 .
正确答案
解析
由图可知,原几何体为长与宽均为4,高为3的正四棱柱中间挖去一个半径为1的圆柱,所以表面积为
考查方向
解题思路
1、还原几何体,表示对应的边长;2、求出表面积,即可得到结果。
易错点
本题易在还原几何体时发生错误。
知识点
5.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如下左图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( )
正确答案
解析
从上向下看,看到的应该是中间的正方形,而四个曲面的边在正方形上的投影在正方形的对角线上,所以得到俯视图是B答案
考查方向
解题思路
从上向下看,看到的应该是中间的正方形,而四个曲面的边在正方形上的投影在正方形的对角线上
易错点
对图形认识不清,误认为俯视图为圆形。
知识点
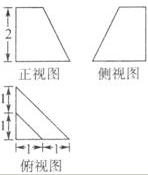
3.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
正确答案
解析
由图可知,
该四棱锥底面边长为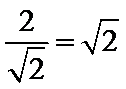
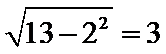
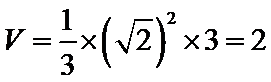
应选B.
考查方向
本题主要考查三视图和锥体的体积公式等知识,考查绘图,识图能力及空间想象能力。难度不大。
解题思路
1.画出立体图形,算出锥体的高;
2.利用体积公式计算,得出结果,应选B。
易错点
1.在求锥体的高时,不能正确找到里面的直角三角形求解;
2.用锥体的体积公式时,易遗漏前面有个1/3。
知识点
扫码查看完整答案与解析