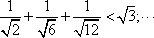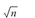- 不等式的应用
- 共23题
16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料。生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元。该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元 .
正确答案
216000（元）
知识点
19.某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元.在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此，搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：
记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），
（I）若
（II）若要求 “需更换的易损零件数不大于
（III）假设这100台机器在购机的同时每台都购买19个易损零件，或每台都购买20个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买19个还是20个易损零件？
正确答案
解：当n=19时 x≤19 y=19×200=3800元
（1）x>19时 y=19×200+(x-19)·500=500x-5700(元)·
∵ y= 
(2)由柱状图知，更换16个频率0.06；更换17件频率为0.16.
更换18件频率为0.24，更换19件频率为0.24 ∴ 更换易损零件不大于n〃的频率为不小于0.5的.则n≥19
∴ n的最小值为19件
(3)若每台都购买19个易损零件，所须费用平均数为
若每台都购买20个易损零件，所须费用平均数为
∴ 购买1台机器的同时应购买19台易损零件.
知识点
12. 已知实数x，y满足
正确答案
知识点
3.已知6双袜子与3双手套的价格之和大于24元，而1双袜子与1双手套的价格之和小于5元，那么2双袜子和3双手套的价格的比较结果是（ ）
正确答案
解析
设一双袜子与一双手套的价格分别为x,y元,则6x+3y>24,得2x+y>8,又x+y<5,所以2x-3y=5(2x+y)-8(x+y)>5×8-8×5=0,故2双袜子的价格高。
知识点
观察下列不等式：
①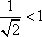
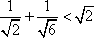
正确答案
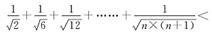
解析
略
知识点
已知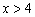
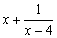
正确答案
6
解析
略
知识点
A0
B
C
D
正确答案
解析
略。
知识点
已知
A
B
C
D
正确答案
解析
略
知识点
已知
A
B
C
D
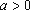
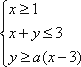
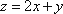
正确答案
解析
略
知识点
9．已知
①
②
③数列
④数列
其中正确的结论是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析