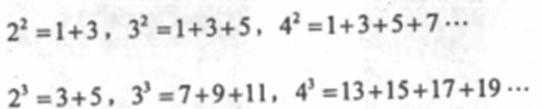- 合情推理与演绎推理
- 共73题
16.对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染16后面最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第60个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一分组数列如下表
现用ai,j表示第i行的第j个数,求a2n,1=( )
正确答案
2n—2行共
解析
解析已在路上飞奔,马上就到!
知识点
已知函数









(1)若对任意的


(2)对于函数






正确答案
见解析
解析
(1)函数


函数


又




不等式

令




故



因此,在对任意的

只需
所以实数

(2)证明:



令



故

令

当






由①②得
又由①得

故函数

知识点
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
, ,, , , , ,
按照以上排列的规律,第 

正确答案
解析
略
知识点
对于大于或等于2的正整数m的n次方幂有如下分解方式:
根据上述分解规律,若m3(m∈N*)的分解中最小的数是91,则m的值为 。
正确答案
10
解析
13=1(1个连续奇数的和),23=3+5(2个连续奇数的和),33=7+9+11 (3个
连续奇数的和),43=13+15+17+19 (4个连续奇数的和),……,
所以,(m-1)3等于m-1个连续奇数的和,因为,m3(m∈N*)的分解中最小的数是91,所
以,(m-1)3的分解中最大的数是89。每个分解中,最大的数+1=2×左边所有的底数的和(从1开始~该分解为止)所以,2×[1+2+……(m-1)]=89+1即,m(m-1)=90化简得,(m-10)(m+9)=0因为,m>0解得,m=10.
知识点
14.定义
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
17. 请你把“若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给出数表
正确答案
2,6,18,54
解析
解析已在路上飞奔,马上就到!
知识点
17. 请你把“若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析