- 功能关系
- 共276题
如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体接触（未连接），弹簧水平且无形变，用水平力F缓慢推动物体，在弹性限度内弹簧长度被压缩了x0，此时物体静止，撤去F后，物体开始向左运动，运动的最大距离为4x0，物体与水平面间的动摩擦因数为μ，重力加速度为g，则（ ）
A撤去F后，物体先做匀加速运动，再做匀减速运动
B撤去F后，物体刚运动时的加速度大小为
C物体做匀减速运动的时间为
D物体开始向左运动到速度最大的过程中克服摩擦力做的功为
正确答案
解析
撤去F后，由于弹力是变力，所以物体在开始的位移x0内不可能做匀变速运动，A项错误；撤去F瞬间，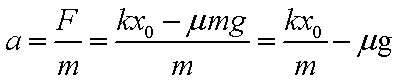
知识点
图18（a）所示的装置中，小物块A.B质量均为m，水平面上PQ段长为l，与物块间的动摩擦因数为μ，其余段光滑。初始时，挡板上的轻质弹簧处于原长；长为r的连杆位于图中虚线位置；A紧靠滑杆（A.B间距大于2r）。随后，连杆以角速度ω匀速转动，带动滑杆作水平运动，滑杆的速度-时间图像如图18（b）所示。A在滑杆推动下运动，并在脱离滑杆后与静止的B发生完全非弹性碰撞。
（1）求A脱离滑杆时的速度uo，及A与B碰撞过程的机械能损失ΔE。
（2）如果AB不能与弹簧相碰，设AB从P点到运动停止所用的时间为t1，求ω得取值范围，及t1与ω的关系式。
（3）如果AB能与弹簧相碰，但不能返回道P点左侧，设每次压缩弹簧过程中弹簧的最大弹性势能为Ep，求ω的取值范围，及Ep与ω的关系式(弹簧始终在弹性限度内)。
正确答案
见解析。
解析
（1）设连杆的水平位移为x 取水平向右的方向为正则：
V0=
AB相碰由动量守恒得：mv0=2mv ②
AB系统机械能损失ΔE=
由①②③得：
（2）AB在pq上做匀减速直线运动，加速度为：
s≤l ⑥
0=v+at1 ⑦
由④⑤⑥⑦得：
（3）AB从p开始到弹簧压缩到最短时过程由能量守恒得：
可得到：
设AB返回时刚好到达P点时速度为0，则此时角速度最大
全过程由能量守恒得：
解得：
知识点
如图是“神舟”系列航天飞船返回舱返回地面的示意图，假定其过程可简化为：打开降落伞一段时间后，整个装置匀速下降，为确保安全着陆，需点燃返回舱的缓冲火箭，在火箭喷气过程中返回舱做减速直线运动，则
正确答案
解析
在火箭喷气过程中返回舱做减速直线运动，加速度方向向上，返回舱处于超重状态，动能减小，返回舱所受合外力做负功，返回舱在喷气过程中减速的主要原因是缓冲火箭向下喷气而获得向上的反冲力。火箭开始喷气前匀速下降拉力等于重力减去返回舱受到的空气阻力，火箭开始喷气瞬间反冲力直接对返回舱作用因而伞绳对返回舱的拉力变小。
知识点
如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连. 弹簧处于自然长度时物块位于O点(图中未标出). 物块的质量为m,AB =a,物块与桌面间的动摩擦因数为
A物块在A点时,弹簧的弹性势能等于
B物块在B点时,弹簧的弹性势能小于
C经O点时,物块的动能小于
D物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能
正确答案
解析
借助弹簧振子的平衡位置的思想，假定AB的中点为C，则因为物体从A到B想做运动的过程中，摩擦力一直做负功，则过O点弹簧的压缩量一直小于OA，即O点在C的左侧，OA>OB，且OA>
知识点
如图所示，倾角θ=300的粗糙斜面固定在地面上，长为
A物块的机械能逐渐增加
B软绳重力势能共减少了
C物块重力势能的减少等于软绳摩擦力所做的功
D软绳重力势能的减少小于其动能增加与客服摩擦力所做功之和
正确答案
解析
选物块为研究对象，细线对物块做负功，物块机械能减小，A错误；物块由静止释放后向下运动，到软绳刚好全部离开斜面，软绳的重心下降了
知识点
扫码查看完整答案与解析