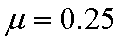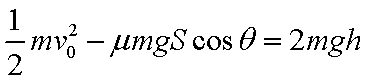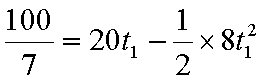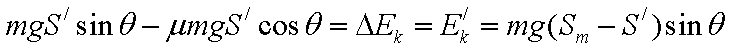- 功能关系
- 共276题
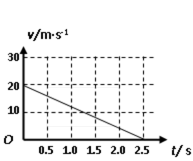
一质量m=0.5kg的滑块以某一初速度冲上倾角为37º且足够长的粗糙斜面,其速度-时间图象如图所示。已知sin37º=0.6,cos37º=0.8,g取10m/s2 求:
(1)滑块与斜面间的动摩擦因数;
(2)上滑后经多长时间滑块的动能与重力势能相等;
(3)滑块返回斜面底端时的动能。
正确答案
(1)初速度为20m/s,由图线知滑块作匀减速直线运动,
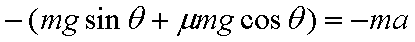
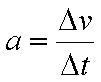
(2) 上滑时经历时间t1动能等于势能,滑至最高点后由于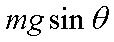
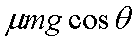
由题设条件及能量关系,上滑时:
S为上滑路程,代入数据求得S = 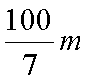
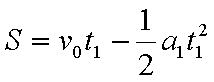
解得
下滑时经
即 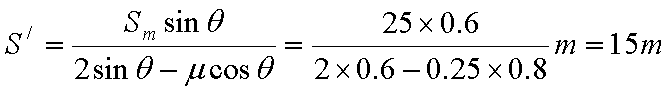
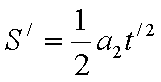
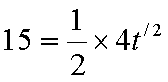
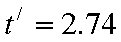
从上滑开始计时有: 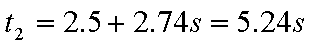
(3) 滑块滑行的总路程为S总=2Sm =50m
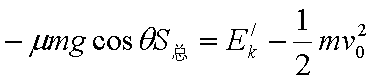
代入数据,求得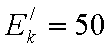
解析
略
知识点
如图,倾角为
正确答案


解析
略
知识点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
26.如右图所示的凹形场地,两端是半径为L的光滑



(1)甲与乙碰撞前的速度;
(2)由于碰撞而损失的机械能;
(3)甲、乙在O处发生碰撞后.刚好不再发生碰撞,甲、乙停在距B点多远处?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.质量为m的带正电小球由空中A点无初速度自由下落,在t秒末加上竖直向上、范围足够大的匀强电场,再经过t秒小球又回到A点,不计空气阻力,且小球从未落地,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图11所示,光滑水平地面上停着一辆平板车,其质量为2 m,长为L,车上右端(A点)有一块静止的质量为m的小金属块。金属块与平板车的上表面之间存在摩擦,以上表面的中点C为界,已知金属块与AC段间的动摩擦因数设为μ,与CB段的动摩擦因数设为μ′,现给车一个向右的水平恒力
(1)撤去力F的瞬间,金属块的速度v1、车的速度v2 分别为多少?
(2)金属块与CB段的动摩擦因数μ′是多少?
正确答案
(1)对金属块,由牛顿第二定律
对车:
则有
联立求解得
(2)以车和金属块为系统撤掉外力后,系统的动量守恒
则有
联立求解得
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,光滑固定斜面倾角为
正确答案
挂钩没有挂D时,A压缩弹簧,弹簧的压缩量为

则
挂钩挂上D后,B刚好离开挡板时弹簧的伸长量为
则

设该过程弹性势能的增量为
将D带电后,D在电场中运动,电场力对D作正功,设B刚离开挡板时D的速度为V,D下降
由以上四个方程消去
得:
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,质量为m的小球P自距离A点4R高处下落,然后沿A点切线方向进入竖直平面内的光滑轨道ABC。AB是半径为R的
(1)小球P和小球Q碰撞时损失的机械能;
(2)整体S离开C点后至撞上圆弧轨道的过程中竖直下落的高度。
正确答案
(1)根据机械能守恒定律,有:
解得:小球P撞击小球Q前的速度
由动量守恒定律
解得:两球的共同速度
(2)因为整体S在C点对轨道的压力恰为零,所以有:
两球离开C点做平抛运动:
解得:
解析
解析已在路上飞奔,马上就到!
知识点
21.绝缘水平面上固定一正点电荷











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析