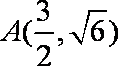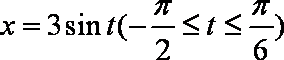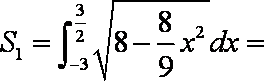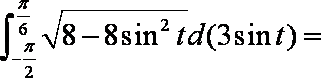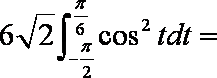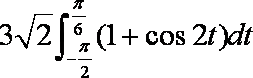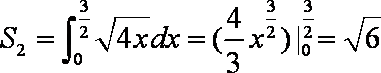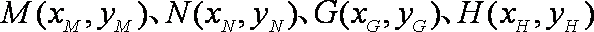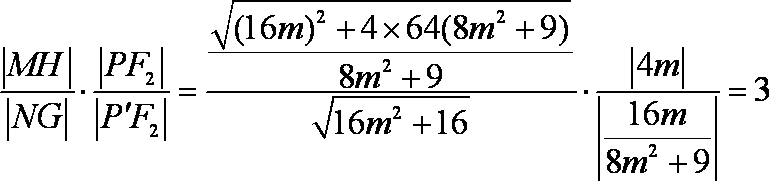- 用定积分求简单几何体的体积
- 共2题
1
题型:简答题
|
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”。
如图,“盾圆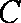
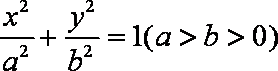

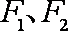
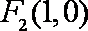
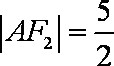
(1)求椭圆的方程;
(2)求定积分时,可以使用下面的换元法公式:函数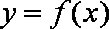
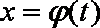
则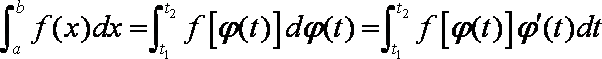
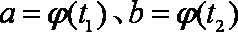
如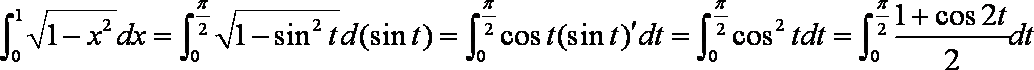
阅读上述文字,求“盾圆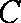
(3)过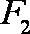
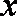
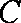
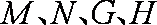
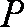
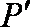
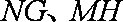
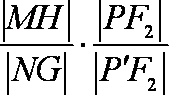
正确答案
见解析
解析
(1)由
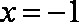
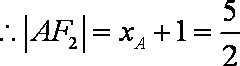
又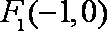
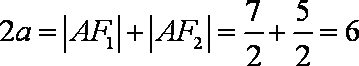
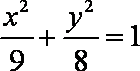
(2)由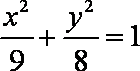
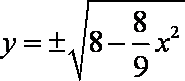
令
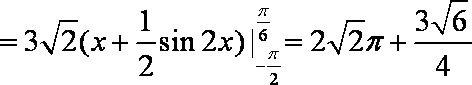
根据对称性, “盾圆
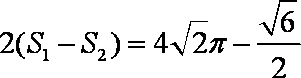
(3)设过

联立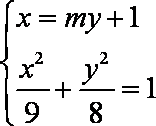
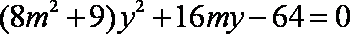
联立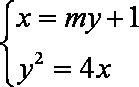
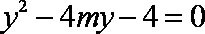
由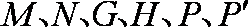
代入韦达定理整理得,
故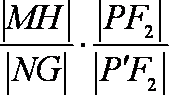
知识点
用定积分求简单几何体的体积
1
题型:填空题
|
12.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
用定积分求简单几何体的体积
已完结
扫码查看完整答案与解析