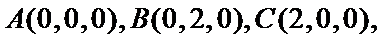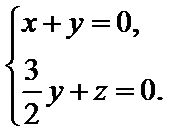- 线面角和二面角的求法
- 共279题
如图,菱形




且
22.求证:

23.若

正确答案
见解析
解析
如图,过点





















考查方向
解题思路
解题步骤如下:做辅助线:过点







平面

易错点
本题易在利用面面垂直证明线面垂直或求法向量时发生错误 。
正确答案
二面角

解析
连接








则


设平面


令

设平面


令




考查方向
解题思路
解题步骤如下:建立空间直角坐标系,根据题目给出的条件,分别求出平面



易错点
本题易在利用面面垂直证明线面垂直或求法向量时发生错误 。
如图,矩形










21.求证:

22.求直线

正确答案
证明见解析
解析
连结OM延长交BF于H,则H为BF的中点,又P为BC的中点,∴PH∥CF,又∵CF

解题思路
根据题意,易证PO∥AC,从而证得PH∥平面AFC
易错点
线面平行中,在面中找线,空间向量的计算不准。
正确答案
解析
设直线AC与平面CEF所成角为
A(0,-1,0),C(0,1,1),E(



令a=2,则

所以直线AC与平面CEF所成角的正弦值为
解题思路
以O为原点,AB为y轴,建立空间直角坐标系,利用空间向量直接求角的正弦
易错点
线面平行中,在面中找线,空间向量的计算不准。
19. 如图,三棱柱ABC-A1B1C1所有的棱长均为2,B1在底面上的射影D在棱长BC上,且A1B∥平面ADC1。
(Ⅰ)求证:平面ADC1⊥平面BCC1B1;
(Ⅱ)求平面ADC1与平面A1AB所成角的正弦值.
正确答案
见解析
解析
(1)证明:
由题意得B1D⊥面ABC,直线ADㄈ面ABC,所以B1D⊥AD
连接A1C交AC1与点E,连接DE,则.
又因为A1B||ADC1
所以A1B||DE
在△A1BC中E是边A1C的中点,所以D为BC的中点
则AD⊥BC
又∵B1D∩BC=B
∴AD⊥平面BCC1B1
∵ADㄈ平面ADC1
∴平面ADC1⊥平面BCC1B1
(2)由(1)得以D为坐标原点,以DC,DA,DA1为xyz轴建系
因为
在平面A1AB中,不共线向量,
设法向量为
同理
在平面ADC1中,不共线向量,
设法向量为
由图知二面角α为锐角
考查方向
主要考察了直线与平面平行的判定与性质,考察了用空间向量求平面间的夹角
解题思路
第一步:根据已知条件A1B∥平面ADC1确定射影D的位置(底边中点)
第二步:根据线面垂直的判定得出:AD⊥平面BCC1B1进而得到面面垂直
第三步:根据第一问证明过程得出以D为坐标原点建系,利用空间向量求出结果
易错点
主要易错于点D位置的确定和面面角正弦值的求解
教师点评
该题思路比较简单,但是有几个关键地方必须考虑清楚:一个是D的位置判断,第二个就是求二面角的过程要细心,看好要求的结果
知识点
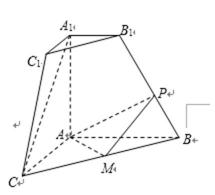
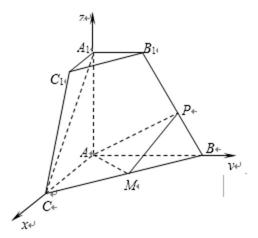
如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=
34.求平面PAB与平面PCD所成二面角的余弦值;
35.点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
正确答案
解析
以A为坐标原点,以AB、AD、AP所在直线分别为x、y、z轴建系A﹣xyz如图,
由题可知B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
(1)∵AD⊥平面PAB,∴
∵

设平面PCD的法向量为
由

取y=1,得
∴cos<



∴平面PAB与平面PCD所成两面角的余弦值为
考查方向
解题思路
(1)所求值即为平面PAB的一个法向量与平面PCD的法向量的夹角的余弦值的绝对值,计算即可;
易错点
本题考查求二面角的三角函数值,在计算过程中易错。
正确答案
解析
(2)∵


又



又




设1+2λ=t,t∈[1,3],
则cos2<




当且仅当t=




因为y=cosx在(0,
又∵BP=



考查方向
解题思路
(2)利用换元法可得cos2<



易错点
本题考查求二面角的三角函数值,考查用空间向量解决问题的能力,在求最值时易错.
如图,在直角梯形
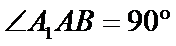
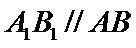
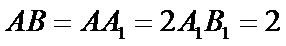
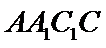
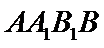
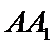
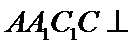

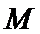

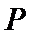
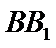
20.求证:
21.当点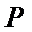
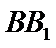
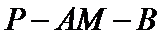
22.是否存在点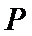
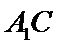
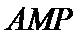
正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
由已知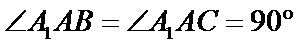
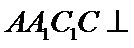

所以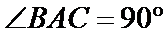
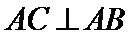
又因为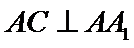
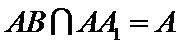
所以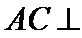
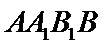
由已知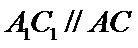
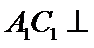
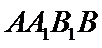
因为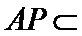
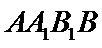
所以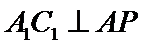
考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“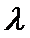
正确答案
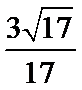
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
(Ⅱ)由(Ⅰ)可知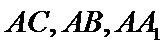
分别以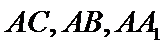
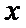

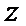
由已知 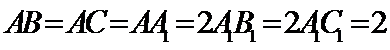
所以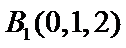
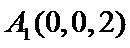
因为

易知平面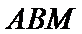

设平面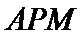
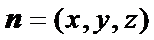
由 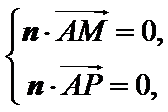
取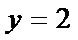
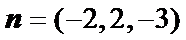
由图可知,二面角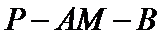
所以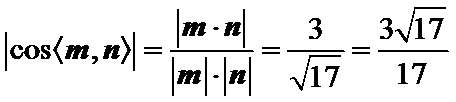
所以二面角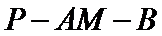
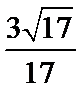
弦值;
考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“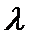
正确答案
在
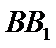
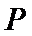
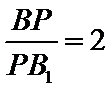
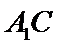
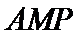
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
存在点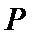
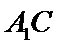
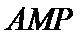
设

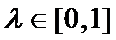

所以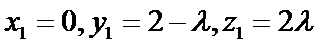
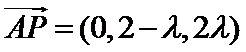
设平面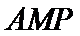
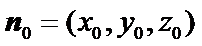
由 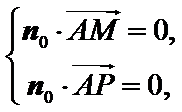
取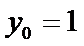
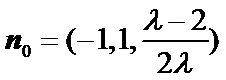
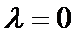
又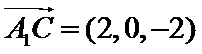
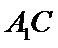
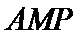
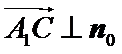
所以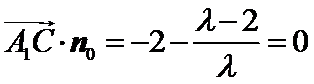
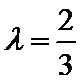
所以在

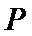
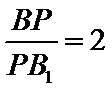

考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“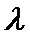
正方体





21.当


22.当平面



正确答案
(1)证明略;(2)
解析




正方体









考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
正确答案
(2)
解析
正方体



分别以





设







则



平面

平面







设平面


则
考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
在四棱锥






21.求直线

22.若





正确答案
详见解析
解析
解(Ⅰ)依题意,以点
不妨设
则






设平面

则

不妨令

所以
∴直线


考查方向
线面平行,线面垂直,直线与平面所成角的三角函数值
解题思路
依据题意,建立空间直角坐标系,用空间向量相关性质计算求解。
易错点
空间感不强,计算能力弱
教师点评
用空间直角坐标系下的空间向量计算是求解立体几何中的问题的一个有效的工具
正确答案
见解析
解析
(Ⅱ)向量

由点



∴
∵

∴

∴
考查方向
向量的运算
解题思路
根据题意写出向量的空间坐标,然后根据立体图形中的线段长等相关性质求解
易错点
计算能力弱
下列关于开放式基金的说法正确的是( )。
A.规模不固定,但有最低规模要求
B.交易手续费为成交金额的2.5%
C.分红方式有现金分红和再投资分红两种
D.单位资产净值于每个开放日进行公告
E.在期限内不能直接赎回基金,须通过上市交易套现
正确答案
A,C,D
解析
[解析] 选项BE描述的是封闭式基金。
如图,四棱锥







22.求证:面

23.设






正确答案
(1)证明:由


有





因为




解析
在梯形ABCD中,BC⊥BD,BC⊥PD,所以BC⊥平面PBD。又BC在平面PBC内,所以PBC⊥平面PBD.
考查方向
考查”两个平面互相垂直的判定定理:若一个平面过另一个平面的垂线,则这两个平面垂直。"
解题思路
根据已知条件及思路,需要在平面PBC内找到一条直线垂直于平面PBD。易证BC⊥BD,BC⊥PD,则得到BC⊥平面PBD。
易错点
难以找到一条直线垂直于另一个平面,或发现了垂直关系,但没有严格证明出现错误。
教师点评
此题考查了证明两个平面垂直的方法,是通过线面垂直而得到的。借此类题,要善于发现垂直关系。
正确答案
由(1)可知


∴



可得

以



设平面

则

设平面

则

所以


19.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马








(1)证明:

(2)若面



正确答案
(1)因为


由底面


所以


又因为



而




又



由




即四面体

(2)如图1,在面





的交线. 由(1)知,

又因为




故


设


在Rt△PDB中, 由

则 

所以
故当面



(解法2)
(1)如图2,以










于是

又已知


因



由







(2)由


由(1)知,


若面


则
解得
故当面



解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析