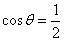- 线面角和二面角的求法
- 共279题
如图,平面ABB1A1为圆柱OO1的轴截面,点C为
(1)求证:B1M∥平面O1AC;
(2)若AB=AA1,∠CAB=30°,求二面角C-AO1 -B的余弦值。
正确答案
见解析
解析
知识点
参数方程

正确答案
解析
略
知识点
如图,已知球




正确答案
解析
略
知识点
如图1,在直角梯形














(1)求证:平面

(2)求直线

(3)在棱



正确答案
见解析
解析
(1)因为点



所以


因为在直角梯形



所以


所以

所以
同理可证
又
所以

(2)在平面


如图建立空间直角坐标系,
则


因为
设平面
因为
所以有

令



所以直线


(3)存在,事实上记点

因为在直角三角形

在直角三角形
所以点

知识点
如图所示,







(1)求证:平面
(2)求证:平面PAC

(3)设二面角


正确答案
见解析
解析
(1)证明:因为点E为线段PB的中点,点

所以 

因为 



所以 
因为 

因为 



所以 
因为 




所以 平面
(2)证明:因为 点C在以AB为直径的⊙O上,
所以 

因为 



所以 
因为 




所以 

因为 

所以 平面PAC

(3)解:如图,以





因为 

所以 

延长


因为 

所以 
所以 



所以 

设平面

因为
所以 
令

所以 
同理可求平面

所以 
所以 
知识点
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BF=
(1)证明:BC⊥平面PAC;
(2)证明:CF⊥BP;
(3)求二面角F﹣OC﹣B的平面角的正弦值。
正确答案
见解析。
解析
(1)证明:∵PA⊥平面ABC,BC⊂平面ABC,∴BC⊥PA。
∵∠ACB是直径所对的圆周角,
∴∠ACB=90°,即BC⊥AC。
又∵PA∩AC=A,∴BC⊥平面PAC。
(2)∵PA⊥平面ABC,OC⊂平面ABC,
∴OC⊥PA。
∵C是弧AB的中点,∴△ABC是等腰三角形,AC=BC,
又O是AB的中点,∴OC⊥AB。
又∵PA∩AB=A,∴OC⊥平面PAB,又PB⊂平面PAB,
∴BP⊥OC。
设BP的中点为E,连接AE,则OF∥AE,AE⊥BP,
∴BP⊥OF。
∵OC∩OF=O,∴BP⊥平面CFO,又CF⊂平面CFO,∴CF⊥BP。
(3)解:由(2)知OC⊥平面PAB,∴OF⊥OC,OC⊥OB,
∴∠BOF是二面角F﹣OC﹣B的平面角。
又∵BP⊥OF,∠FBO=45°,∴∠FOB=45°,
∴

知识点
如图,在四棱锥







(1)当




(2)求证:平面

(3)当二面角




正确答案
见解析
解析
(1)证明:连接


因为



所以

(2)证明:由(1)知

建立如图所示的空间直角坐标系.
设四棱锥
则





所以

设


所以

设平面

则
令

易知

因为
所以


(3)解:设

平面

因为
所以

由已知二面角

所以
所以

所以点

知识点
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=

(1)求证:PA⊥CD;
(2)求二面角C﹣PB﹣A的余弦值。
正确答案
见解析。
解析
:(1)
连接OC,由3AD=BD知,点D为AO的中点,
又∵AB为圆的直径,∴AC⊥BC,
∵
∴△ACO为等边三角形,∴CD⊥AO。
∵点P在圆O所在平面上的正投影为点D,
∴PD⊥平面ABC,又CD⊂平面ABC,
∴PD⊥CD,PD∩AO=D,
∴CD⊥平面PAB,PA⊂平面PAB,
∴PA⊥CD。
(2)
过点D作DE⊥PB,垂足为E,连接CE,
由(1)知CD⊥平面PAB,又PB⊂平面PAB,
∴CD⊥PB,又DE∩CD=D,
∴PB⊥平面CDE,又CE⊂平面CDE,
∴CE⊥PB,
∴∠DEC为二面角C﹣PB﹣A的平面角。
由(1)可知CD=
∴PB=3


∴在Rt△CDE中,tan∠DEC=

∴cos∠DEC=

知识点
如图,直角梯形





(1)求证:
(2)求直线

(3)线段



正确答案
见解析
解析
(1)证明:取



因为

因为四边形


所以四边形

所以

所以
(2)解:因为平面


所以


由

因为三角形



所以 


设直线


所以
即直线


(3)解:存在点



证明如下:由


设平面

所以 


因为 




即点



知识点
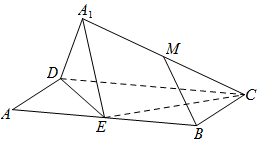
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE。
(1)当平面A1DE⊥平面BCD时,求直线CD与平面CEA1所成角的正弦值;
(2)设M为线段A1C的中点,求证:在△ADE翻转过程中,BM的长度为定值。
正确答案
见解析。
解析
解:
(1)过A1作A1F⊥DE,由已知可得A1F⊥平面BCD,且F为DE中点,以D为原点,DC、DA所在直线为
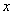

求得平面CEA1的一个法向量为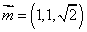
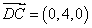
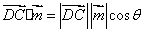
所以,直线CD与平面CEA1所成角的正弦值为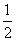
(2)取A1D中点G,连结MG,EG,由MG∥EB,且MG=EB,可得BMGE为平行四边形,所以,BM=EG,而三角形ADE中,EG的长度为定值,所以,BM的长度为定值。
知识点
扫码查看完整答案与解析