函数奇偶性的判断
共55题

· 函数奇偶性的判断

函数奇偶性的判断
共55题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

8.设函数则是

A奇函数，在（0,1）上是增函数

BB．奇函数，在（0,1）上是减函数

C．偶函数，在（0,1）上是增函数

D．偶函数，在（0,1）上是减函数

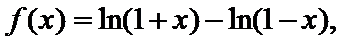
正确答案

解析

显然，f(x)的定义域为（-1,1），关于原点对称，又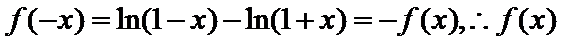为奇函数，显然，f(x)在（0,1）上单调递增，故选A.

考查方向

本题主要考察函数的单调性和奇偶性等知识，意在考察考生对于函数性质的理解。.

解题思路

分求函数的定义域后发现其关于原点对称，后利用奇偶性的定义得到其为奇函数，最后利用奇函数在对称的区间上单调性相同，得到其单调性。

易错点

对于函数的性质不理解导致出错。

知识点

函数的单调性及单调区间函数奇偶性的判断利用导数研究函数的单调性

题型：单选题

单选题 · 5 分

7．已知函数, ，为常数，给出下列四种说法：

①的值域是；

②当时，的所有零点之和等于；

③当时，有且仅有一个零点；

④是偶函数.

其中正确的是（）

A①③

B①④

C②③

D②④

正确答案

解析

由图像可知函数的值域为，故①错误；当时，由可知或或，解得函数的零点为，故所有零点之和等于，②正确；由图像可知，当时，，故直线与函数有且仅有一个交点，故此时函数有以个零点，③正确，所以本题选择C选项。

考查方向

本题主要考查了分段函数的图像及性质、数形结合思想、函数的零点等知识点，为高考常考题，在近几年的各省高考题出现的频率较高，常与函数的性质、函数的零点、函数的图像等知识点交汇命题。

解题思路

先画出函数的图像，再根据图像及函数的相关性质即可作出本题。

易错点

不能准确画出函数的图像导致本题出错。

知识点

分段函数的解析式求法及其图象的作法函数单调性的判断与证明函数奇偶性的判断二次函数的零点问题

题型：单选题

单选题 · 5 分

3.下列函数中，既是奇函数，又是在区间上单调递减的函数为（）

正确答案

解析

A. 定义域为，，偶函数，在上单调递减；B. 定义域为，，奇函数，在上单调递减；

C. 定义域为R，非奇非偶 D. 定义域为R，奇函数，在上单调递增，所以选项B为正确选项

考查方向

本题主要考查了函数的性质

解题思路

先求定义域，判断奇偶性，再利用性质判断单调性

易错点

本题易在函数指数函数、对数函数、幂函数混淆

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

3.设是定义在R上的函数,则“不是奇函数”的充要条件是

正确答案

解析

由奇函数的定义知：，则为奇函数，其逆否命题为：不是奇函数，则，故选C。

考查方向

本题主要考查逆否命题的真假、奇函数的定义、全特称命题的否定等知识，意在考查考生的逻辑推理能力和转化与化归的能力。

解题思路

先根据奇函数的定义得到题中命题的逆否命题；根据逆否命题求出本题的答案。

易错点

全称命题的否定形式写错；不能正确理解不是奇函数的条件；

知识点

含有逻辑联结词命题的真假判断函数奇偶性的判断函数奇偶性的性质

题型：单选题

单选题 · 5 分

6.下列函数中，既是奇函数，又在区间上单调递减的函数是（）

正确答案

解析

A选项是奇函数，在区间上单调递增，故错误；B选项是偶函数，在区间上不单调，故错误；C选项是非奇非偶函数，在区间上单调递增，故错误；

D选项是奇函数，在区间上单调递减，A、Ｂ、Ｃ选项不对，所以选D选项。

考查方向

本题主要考查了函数的性质：奇偶性、单调性/函数的性质的综合考查在高考中经常出现，主要涉及区间转换法求解析式、比较大小、求参数取值或范围、解不等式等，主要考查单调性、奇偶性、对称性的综合应用，属于中档题。

解题思路

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

单选题 · 5 分

3.下列函数中，既不是奇函数，也不是偶函数的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 函数奇偶性的性质

百度题库 > 高考 > 文科数学 > 函数奇偶性的判断

扫码查看完整答案与解析