- 函数奇偶性的性质
- 共114题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
定义域为R的偶函数
A
B
C
D
正确答案
解析
略。
知识点
偶函数y=f（x）的图象关于直线x=2对称，f（3）=3，则f（﹣1）=
正确答案
3
解析
因为偶函数y=f（x）的图象关于直线x=2对称，所以f（2+x）=f（2﹣x）=f（x﹣2），
即f（x+4）=f（x），则f（﹣1）=f（﹣1+4）=f（3）=3
知识点
函数
正确答案
2
解析
略
知识点
若f(x)＝(x＋a)(x－4)为偶函数，则实数a＝__________.
正确答案
4
解析
f(x)＝x2＋(a－4)x－4a.因为f(x)为偶函数，所以f(－x)＝x2＋(4－a)x－4a＝x2＋(a－4)x－4a，a－4＝4－a，a＝4
知识点
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x，则函数g（x）=f（x）﹣x+3的零点的集合为（ ）
A{1，3}
B{﹣3，﹣1，1，3}
C{2﹣
D{﹣2﹣
正确答案
解析
∵f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣3x，
令x＜0，则﹣x＞0，
∴f（﹣x）=x2+3x=﹣f（x）
∴f（x）=﹣x2﹣3x，
∴
∵g（x）=f（x）﹣x+3
∴g（x）=
令g（x）=0，
当x≥0时，x2﹣4x+3=0，解得x=1，或x=3，
当x＜0时，﹣x2﹣4x+3=0，解得x=﹣2﹣
∴函数g（x）=f（x）﹣x+3的零点的集合为{﹣2﹣
知识点
下列函数中，既是奇函数又是增函数的为（ ）
A。
B
C
D
正确答案
解析
A是增函数，不是奇函数；B和C都不是定义域内的增函数，排除，只有D正确，因此选D.
知识点
下列函数中，对于任意
A
B
C
D
正确答案
解析
略
知识点
设函数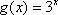
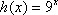
（1）解方程：
（2）令
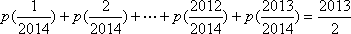
（3）若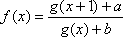
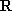
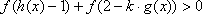
正确答案
见解析
解析
（1）
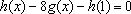
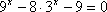
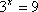
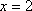
（2）
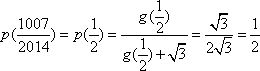
因为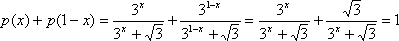
所以，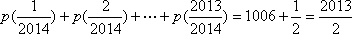
（3）因为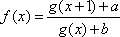
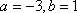
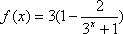
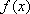
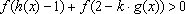
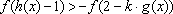
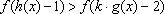
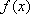
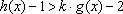
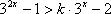
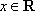
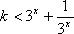
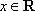
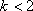
知识点
若集合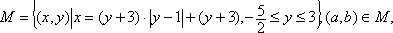
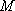
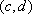
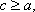
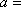
正确答案
解析
略
知识点
扫码查看完整答案与解析