- 指数函数的图像变换
- 共416题
19. 如图,





(Ⅰ)求证:

(Ⅱ)在棱




正确答案
【法一】(Ⅰ)在线段



则


∴




∴
(Ⅱ)由



过点



则

在






∴
∴



故棱


【法二】建立如图所示的空间直角坐标系,
则





∴





(Ⅰ)∵


∴
(Ⅱ)取


∴



同理,取


∴






又∵

∴



故棱



解析
解析已在路上飞奔,马上就到!
知识点
3. 以下有关命题的说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知f (x)=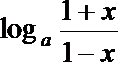
(1)求f (x)的定义域;
(2)判断f (x)的奇偶性并给予证明;
(3)求使f (x)>0的x的取值范围
正确答案
(1) 由 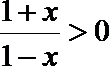
∴ f (x)的定义域为(-1,1)
(2) ∵ f (x)的定义域为(-1,1)关于原点对称;
且 f (-x)=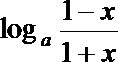
∴ 函数y=f (x)是奇函数;
(3) 由f (x)=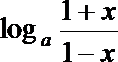
若a>1, 则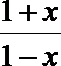
即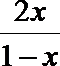
∴ 0<x<1;
若0<a<1, 则 0<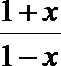
∴-1<x<0
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)求函数
(2)求函数
正确答案
(1)由函数的图像经过点(0,2)可知,
∴ f(x)=x3+bx2+cx+2
∴ f ′(x)=3x2+2bx+c
∵ 

∴ 
故所求的解析式是
(2)由(1)∴ f′(x)=3x2- 6x -3
令3x2- 6x -3=0 ,即 x2-2x -1=0
解得 x1=
当x< 

当

故函数
(-∞,

单调递减区间是(

解析
解析已在路上飞奔,马上就到!
知识点
19.用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少
正确答案
设容器的高为xcm,容器的体积为V(x)cm3,
则V(x)=(90-2x)(48-2x)x,
V(x)=4x3-276x2+4320x (0<V<24)
∵ V′(x) =12 x2-552x+4320=12(x-10)(x-36)
由V′(x)=0得x1=10,x2=36 (舍去)
∵ 当0<x<10 时,V′(x)>0,那么V(x)为增函数
当10<x<24时,V′(x)<0, 那么V(x)为减函数
所以,当x=10, V(x)有极大值V(10)=10(90-20)(48-20)=1960
又V(0)=0,V(24)=0,
所以当x=10, V(x)有最大值V(10)=1960
∴ 容器的高为10cm时,容器的容积最大,最大容积是1960cm3
解析
解析已在路上飞奔,马上就到!
知识点
1.已知



正确答案
2-i
解析
解析已在路上飞奔,马上就到!
知识点
2.已知线性方程组的增广矩阵为


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
9.有一个正四面体的棱长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

































