- 导数与积分
- 共1403题
已知函数f(x)=ax2﹣2x+lnx。
(1)若f(x)无极值点,但其导函数f'(x)有零点,求a的值;
(2)若f(x)有两个极值点,求a的取值范围,并证明f(x)的极小值小于
正确答案
见解析。
解析
(1)首先,x>0
f′(x)有零点而f(x)无极值点,表明该零点左右f′(x)同号,故a≠0,且2ax2﹣2x+1=0的△=0.由此可得
(2)由题意,2ax2﹣2x+1=0有两不同的正根,故△>0,a>0。
解得:
设2ax2﹣2x+1=0的两根为x1,x2,不妨设x1<x2,
因为在区间(0,x1),(x2,+∞)上,f′(x)>0,
而在区间(x1,x2)上,f′(x)<0,故x2是f(x)的极小值点。
因f(x)在区间(x1,x2)上f(x)是减函数,如能证明
由韦达定理,
令

利用导数容易证明g(t)当t>1时单调递减,而g(1)=0,
∴g(t)=lnt﹣

因此f(

从而有f(x)的极小值f(x2)<﹣
知识点
设函数




(1)求
(2)求
正确答案
见解析。
解析
(1)由函数

∴

∴

∴

∴
(2)由(1)知

由

∴
知识点
设函数
(1)已知曲线




(2)讨论函数
(3)在(1)的条件下,求证:对于定义域内的任意一个

正确答案
见解析
解析
(1)


根据题意,
所以

解得
(2)
1)当



所以


2)当
若




若





综上所述,当







(3)由(1)可知
设


当






可见
所以



知识点
对于每一个正整数





正确答案
-2
解析
知识点
设



(1) 求证: 
(2) 若

正确答案
见解析
解析
解: (1)因为

(2)因为
所以
又由

所以
由(1),得
知识点
直线

正确答案
解析
直线





知识点
设曲线






(1)求
(2)求函数
(3)求证:
正确答案
见解析。
解析
(1)



(2)


又

(3)证明:
∴原式





知识点
过点(﹣1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程是 。
正确答案
y=x+1
解析
设切点为(a,ea)
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y﹣ea=ea(x﹣a),代入点(﹣1,0)得:
﹣ea=ea(﹣1﹣a),
解得a=0
因此切线为:y=x+1。
知识点
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列
正确答案
解析
由f(x)=x2+bx求导得:f′(x)=2x+b,
∵函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,
∴f′(1)=2+b=3,∴b=1,∴f(x)=x2+x
所以f(n)=n(n+1),
∴
∴S2013的值为1﹣





知识点
已知函数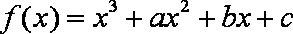
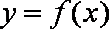
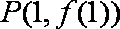
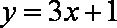
(1)若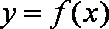
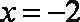
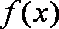
(2)若函数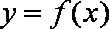
正确答案
见解析。
解析
(1)由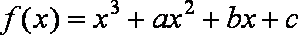
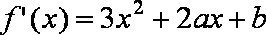
过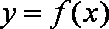
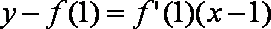
即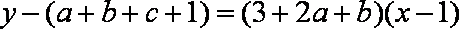
而过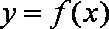
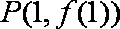
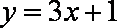
故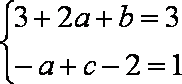
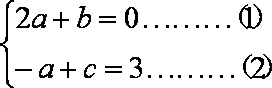
因为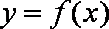
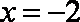
故
由(1)(2)(3)联立解得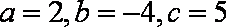
所以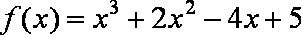
(2)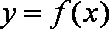
又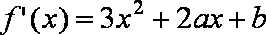
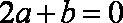
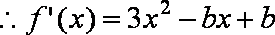
依题意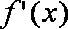
即
①在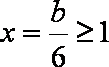
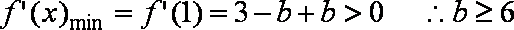
②在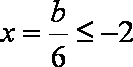
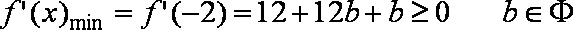
③在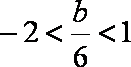
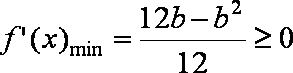
综合上述讨论可知,所求参数b的取值范围是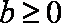
知识点
扫码查看完整答案与解析