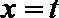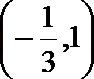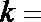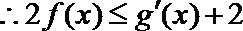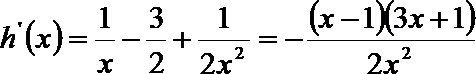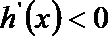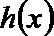- 导数与积分
- 共1403题
21.设函数


(1)若

(2)若直线




(3)若在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.曲线

正确答案
y=3x+1
解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)若

(2)若函数



(3)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数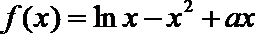
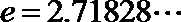
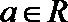
(Ⅰ)当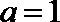
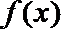
(Ⅱ)若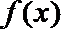
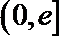
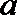
(Ⅲ)设函数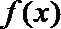
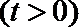
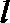
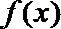
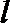
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在
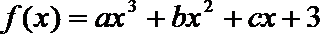
① 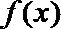
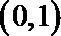
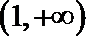
② 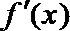
③ 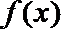
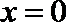
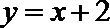
(1)求函数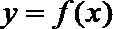
(2)设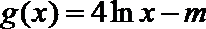
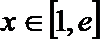
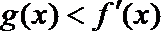
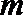
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知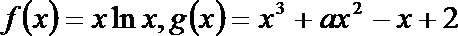
(I)如果函数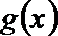
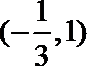
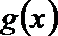
(II)在(Ⅰ)的条件下,求函数y=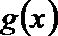
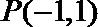
(III)若不等式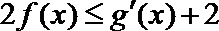
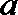
正确答案
解: (I)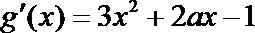
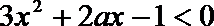
即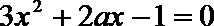
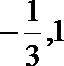
将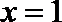
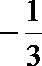
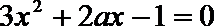
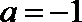
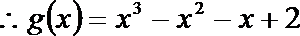
(II)由(Ⅰ)知: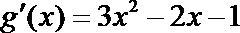
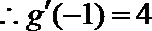
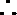
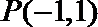
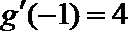
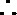
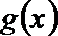
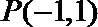
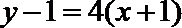
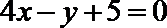
(III)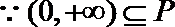
即: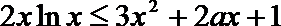
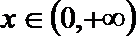
可得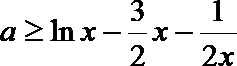
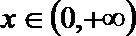
设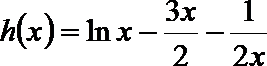
令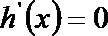
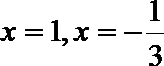
当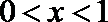
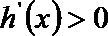
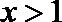
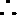
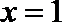
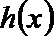
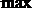
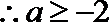
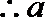
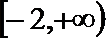
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)当

(2)设|MN|=

(3)在(2)的条件下,若对任意的正整数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若曲线
正确答案
(1,0)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析