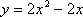- 导数与积分
- 共1403题
若函数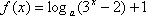
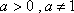
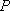
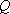
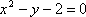
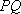
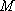
正确答案
解析
略
知识点
已知斜率为2的直线


正确答案
解析
抛物线的焦点坐标是










知识点
将一颗骰子先后投掷两次分别得到点数


正确答案
解析
依题意,将一颗骰子先后投掷两次得到的点数所形成的数组







知识点
已知函数




(1)确定

(2)若

(3)设斜率为



证明:
正确答案
见解析。
解析
(1)依题意得
由函数



(2)由(1)得
∵函数
∴当
由



即函数

当



若






即函数



若






即函数



若



即函数

综上得:当


当




当


当




(3)证法一:依题意得
证
因
令



令

∴

∴


综①②得


证法二:依题意得


由










证法三:令

当



∴当


同理,令
证法四:依题意得

令
当



∴当



当



∴当


所以命题得证
知识点
已知函数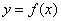
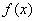
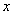
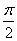
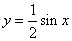
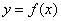
正确答案
解析
对函数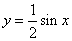
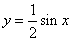
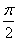
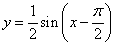
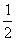
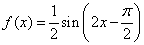
知识点
已知函数
(1)若

(2)设


正确答案
(1)
解析
解析:
(1)因为
则 

平方得,

所以 
(2)因为
=
=
=
当

所以,当


当


知识点
已知函数

(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值;
(2)求函数h(x)=f(x)+g(x)的单调递增区间。
正确答案
见解析。
解析
(1)先对函数f(x)根据二倍角公式进行化简,再由x=x0是函数y=f(x)图象的一条对称轴求出x0的值后代入到函数g(x)中,对k分奇偶数进行讨论求值。
(2)将函数f(x)、g(x)的解析式代入到h(x)中化简整理成y=Asin(wx+ρ)+b的形式,得到h(x)=

解:(1)由题设知
因为x=x0是函数y=f(x)图象的一条对称轴,所以
即
所以
当k为偶数时,
当k为奇数时,
(2)
=
=
当

函数
故函数h(x)的单调递增区间是
知识点
已知函数




(1) 求
(2) 求函数
(3) 若函数

正确答案
见解析
解析
(1) 函数f (x)的定义域为(0,+∞)……1分
∵ f ′ (x) =
∴
(2)由(1) 知
∴ f ′ (x) =
由f ′ (x) > 0可得x >2或x <1,由f ′ (x) < 0可得1< x <2。
∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ),
单调递减区间为 (1 , 2 )。 ………9分
(3) 由(2)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增。
且当x =1或x =2时,f ′ (x) = 0。 ………10分
∴ f (x) 的极大值为 
f (x)的极小值为
由题意可知
则 
知识点
已知函数





(1)当

(2)求证:函数

(3)解析:答本小题考生只需从下列三个问题中选择一个写出结论即可(无需写解析:题步骤),注意:考生若选择多于一个问题解析:答,则按分数最低一个问题的解析:答正确与否给分。
① 当

② 当




③ 当



正确答案
见解析
解析
(1)∵



又当



(2)证明∵对于

∴

又∵
∴


(3)依据选择解析:答的问题评分
①

③
知识点
某省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数




(1)令

(2)若用每天


(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染
指数是否超标?
正确答案
见解析
解析
解析:(1)单调递增区间为

证明:任取



所以函数


(2)由函数的单调性知
∴


当
则
∵


且
故
(3)因为当且仅当

故当

知识点
扫码查看完整答案与解析