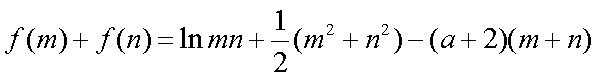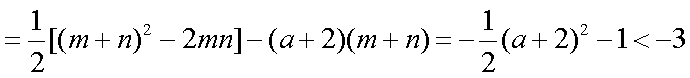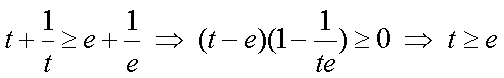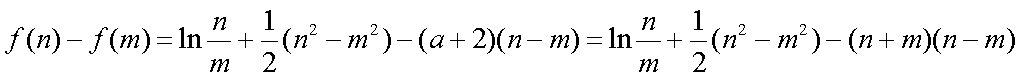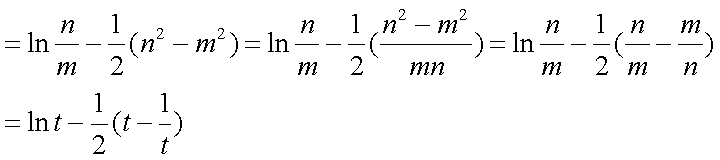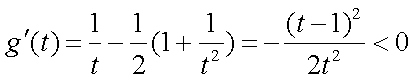- 导数与积分
- 共1403题
已知在




(1)求
(2)若

正确答案
见解析。
解析
(1)由所给条件,方程



(2) ∵ 

由(1)知,





由正弦定理
得
知识点
已知函数
(1)若曲线





(2)在(1)的条件下,试求函数


(3)若


正确答案
见解析。
解析
(1)












由①②得:
(2)由(1)知:




当





由表可知:

当




由表可知:

综上可知:当


当

(3)因为


即

∴
由 (1)+(3)得:
由(4)得:



故
知识点
在平面直角坐标系

















(1)求椭圆
(2)若点


(3)记




正确答案
见解析。
解析
(1)由题意,得

又




(2)






联立方程组





(3)当

当
























知识点
已知直线


(1)求a,b的值;
(2)若函数










设C1在点M处的切线的斜率为



正确答案
见解析
解析
解:(1)直线

又


(2)

∴

由


则

又
法一:令


因为





则

法二:令


因为


故



于是

故






知识点
定义:

正确答案
解析
由F(x,y)的定义知,an=(n∈N*),∵对任意正整数n,都有an≥ak成立,∴ak为数列{an}中的最小项,由指数函数与幂函数的增大速度及a1=2,a2=1,a3=,a4=1知,当a>4时,恒有an>1,∴对∀n∈N*,有an≥a3=成立
知识点
已知函数
(1)试求b,c所满足的关系式;
(2)若b=0,方程
(3)若b=1,集合
正确答案
见解析
解析
(1)由
∴b、c所满足的关系式为
(2)由


方程


令


令


当


当





由函数



故所求


(3)由






当



当





当


注:可直接通过研究函数

知识点
已知


正确答案
解析


知识点
设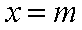
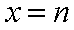
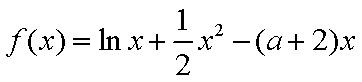
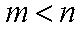
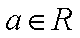
(1) 求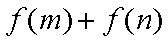
(2) 若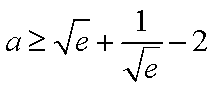
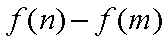
注:e是自然对数的底数。
正确答案
见解析
解析
(1)解:函数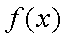
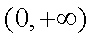
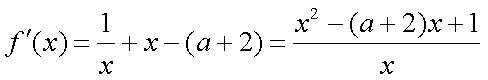
依题意,方程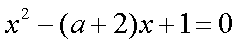
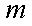
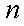
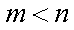
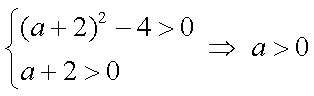
并且 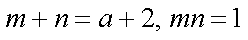
所以,
故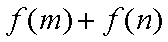
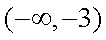
(2)解:当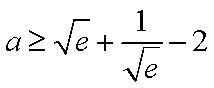
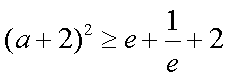
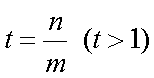
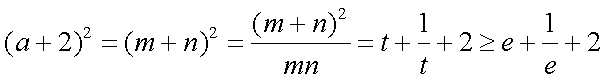
于是有
构造函数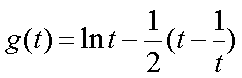
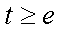

所以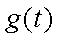
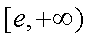
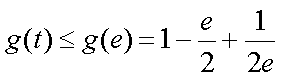
故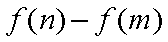
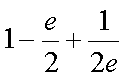
知识点
已知函数
(1)求函数
(2)令


正确答案
见解析
解析
(1)∵
∴

又

∴

故

(2)
定义域
则
设


由于



∴
又

由

∴只需
知识点
已知函数
(1)当


(2)当

正确答案
见解析。
解析
(1)当








(2)因为
所以

令
(Ⅰ)当

所以当



当



(Ⅱ)当

解得:
①若



②若






③ 当







综上所述:
当



当


当



知识点
扫码查看完整答案与解析