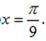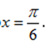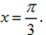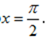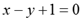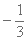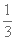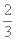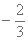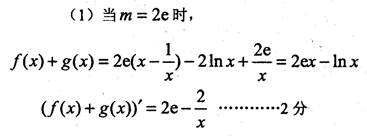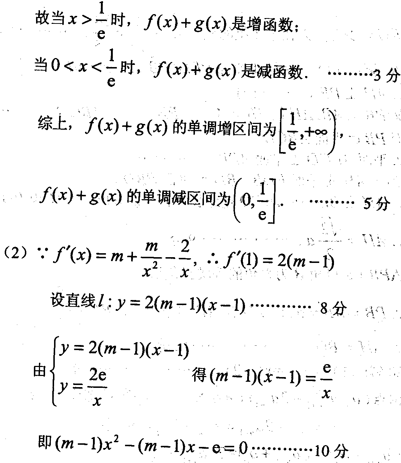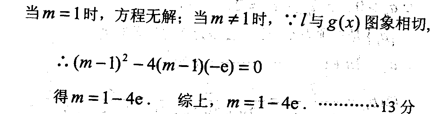- 导数与积分
- 共1403题
曲线

正确答案
解析
直线





知识点
已知曲线



正确答案
解析
略
知识点

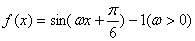
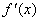
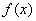
正确答案
解析
略
知识点
已知函数





(1)求
(2)若函数

正确答案
见解析。
解析
(1)由





又∵曲线


由<1><2><3>可求得,
(2)若函数




∴方程
解得:

所以当实数


知识点
曲线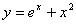
正确答案
解析
略
知识点
已知曲线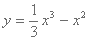
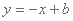
正确答案
解析
略
知识点
已知f (x) = x3 – ax,x∈R,在x = 2处的切线垂直于直线x + 9y – 1 = 0, 则a =( )
正确答案
解析
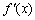
则k=9,∴12-a=9,即a=3。
知识点
已知曲线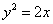
正确答案
1
解析
略
知识点
已知函数

(1)若曲线



(2)求函数
正确答案
见解析
解析
(Ⅰ)由

且

解得
(2)
令


(i)当





则函数


(ii)当




则函数


令

则函数

(iii)当




(iiii)当




则函数


令

则函数

知识点
设函数f(x)=m(x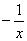
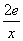
(1)当m=2e时,求f(x)+g(x)的单调区间;
(2)若直线l与函数f(x),g(x)的图象都相切,且与函数f(x)的图象相切于点(1,0),求m的值。
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析