- 线面角和二面角的求法
- 共51题
如图,在四棱锥A—BCDE中,平面





(1)证明:

(2)求直线
正确答案
见解析
解析
证明:(1)连接



由

又平面


(2)在直角梯形


又平面


做








在


在


在


所以,直线

知识点
如图,在三棱锥







(1)求直线

(2)求二面角
正确答案
(1)
(2)
解析
(1)连接OC. 由已知,
设AB的中点为D,连接PD、CD.
因为AB=BC=CA,所以CD
因为
不妨设PA=2,则OD=1,OP=
所以CD=2

在Rt

(2)过D作DE
由已知可得,CD
据三垂线定理可知,CE⊥PA,
所以,
由(1)知,DE=
在Rt△CDE中,tan
故
知识点
把正方形ABCD沿对角线BD折成直二面角,对于下面结论:①AC⊥BD;②CD⊥平面ABC;③AB与BC成600角;④AB与平面BCD成450角。则其中正确的结论的序号为
正确答案
解析
略
知识点
设














正确答案
解析
若












若





则p∨q,为真命题,p∧q,(¬p)∧(¬q),p∨(¬q)都为假命题
知识点
如图,四棱锥





(1)证明:
(2)求AB与平面SBC所成角的大小。
正确答案
见解析。
解析
解法一:(1)
取







又

所以
由








所以

另解:由已知易求得






(2)由



作



作


连结

又




作







由于






设




解法二:以



设


又设

(1)

由

故
由

又由

即

于是

故

所以

(2)设平面

则
又
故
取


故


知识点
一个圆锥的底面积为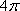
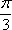
正确答案
解析
略
知识点
已知平面α截一球面得圆M,过圆心M且与α成60°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )
正确答案
解析
知识点
正方体ABCD-A1BCD1中,BB1与平面ACD1所成角的余弦值为
正确答案
解析
本题考查了立体几何中线面角的求法. 










知识点
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D。
(1)求证:PB1∥平面BDA1;
(2)求二面角A-A1D-B的平面角的余弦值;
正确答案
见解析
解析
解法一:
(1)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又OD面BDA1,PB1面BDA1,
∴PB1∥平面BDA1。
(2)过A作AE⊥DA1于点E,连结BE,∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C,由三垂线定理可知BE⊥DA1。
∴∠BEA为二面角A-A1D-B的平面角。
在Rt△A1C1D中,
又

在Rt△BAE中,

故二面角A-A1D-B的平面角的余弦值为
解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则




(1)在△PAA1中有

∴


设平面BA1D的一个法向量为
则


∵
∴PB1∥平面BA1D,
(2)由(1)知,平面BA1D的一个法向量
又

故二面角A-A1D-B的平面角的余弦值为
知识点
如图,在底面是菱形的四棱锥





(1)求证:

(2)求证:平面

(3)求二面角
正确答案
见解析。
解析
(1)连接BD,交AC于点O,连接OE,在三角形BDP中,







(2)


又








(3)过点



由(2)知,







易得:
知识点
扫码查看完整答案与解析