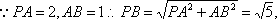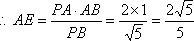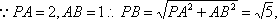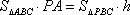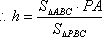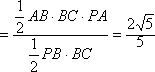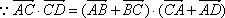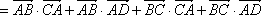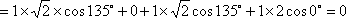- 线面角和二面角的求法
- 共51题
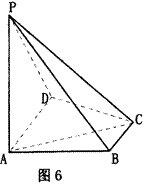
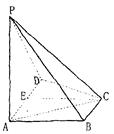
如图6,已知四棱锥P-ABCD中
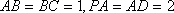
(1)求PC与平面PAB所成角的正切值;
(2)求证:平面PAC⊥平面PCD.
正确答案
见解析。
解析
(1)解法一:∵PA⊥平面ABCD,BC 
又∵BC⊥AB,PA∩AB=A ∴BC⊥平面PAB
又∵BC
在平面PAB内过点A作AE⊥PB于E,则AE⊥平面PBC,
∴AE的长为点A到与平面PAC的距离
在Rt△PAB
解法二:∵PA⊥平面ABCD,AD 
又∵DA⊥AB,PA∩AB=A ∴AD⊥平面PAB
∵BC⊥AB ∴BC∥AD ∴BC⊥平面PAB ∴BC⊥PB
在Rt△PAB
设点A到平面PBC的距离为h,则由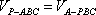
(2)证法一:
过点C作CE∥AB交AD于点E,
∵DA⊥AB ∴DA⊥EC,且AE =BC =1
∵AD =2,∴E为AD的中点,∴EC为AD的垂直平分线,
∴CD=AC,∵△ABC为等腰直角三角形,∴∠BAC=450
∴∠DAC =∠ADC=450,∴∠DCA=900,即DC⊥AC,
又∵PA⊥平面ABCD,CD
且PA∩AC=A,
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD
证法二:∵PA⊥平面ABCD,CD
又
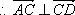
又∵PA⊥平面ABCD,CD
∴CD⊥平面PAC,∵CD
∴平面PAC⊥平面PCD.
知识点
如图,四棱锥


(1)平面PAD与平面PAB是否垂直?并说明理由;
(2)求直线PC与平面ABCD所成角的正弦值。
正确答案
见解析。
解析
(1)平面
∵
∵四棱锥

∵






∵




平面

(2)如图,过点




由(1)可知
∵
∴平面
∵



平面

∴
∴


∴






在直角三角形
故
在直角三角形

故直线


知识点
如图,在斜三棱柱






(1)求
(2)证明EA1∥平面
正确答案
见解析。
解析
(1)解:过










因为


又因为



因此,由三垂线定理
因为


于是为


由于四边形
所以,


(2) 证明:设


在平行四边形

而EP





知识点
如图所示,PA⊥平面ABCD,ABCD是矩形,AB = 1,
(1)若

(2)若二面角



正确答案
见解析
解析
(1)证明:

∴
又


又

∴

∴

而

(2)由(1)知:

∴


∴
∴

即


知识点
9.已知圆锥的底面半径


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析