圆与方程_章节学习

1

题型：简答题

|

简答题

如图，延长⊙O的半径OA到B，使OA=AB，DE是圆的一条切线，E是切点，过点B作DE的垂线，垂足为点C．

求证：∠ACB=∠OAC．

正确答案

解：如图，取EC的中点F，连接AF，OE，AE．

则OE⊥EC，AF∥OE．

∴AF⊥EC．

∴∠CAF=∠EAF．

又∵OE∥AF∥BC，

∴∠EAF=∠OEA=∠OAE，

∠CAF=∠ACB．

∴∠OAE=∠EAF=∠CAF=∠ACB．

∴∠ACB=∠OAC．

解析

解：如图，取EC的中点F，连接AF，OE，AE．

则OE⊥EC，AF∥OE．

∴AF⊥EC．

∴∠CAF=∠EAF．

又∵OE∥AF∥BC，

∴∠EAF=∠OEA=∠OAE，

∠CAF=∠ACB．

∴∠OAE=∠EAF=∠CAF=∠ACB．

∴∠ACB=∠OAC．

1

题型：填空题

|

填空题

如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过P点作⊙O的切线，切点为C，连接AC，若∠CPA=30°，PC=______cm．

正确答案

解析

解：连接OC，

PC是⊙O的切线，

∴∠OCP=90°

∵∠CPA=30°，OC==3，

∴tan30°=，

即PC=．

故填：．

1

题型：简答题

|

简答题

如图，AB是圆O的直径，AC是弦，∠BAC的平分线AD交圆O于点D，DE⊥AC且交AC的延长线于点E．

求证：DE是圆O的切线．

正确答案

证明：连接OD，

∵OA=OD，∴∠ODA=∠OAD

∵∠BAC的平分线是AD

∴∠OAD=∠DAC

∴∠DAC=∠ODA，可得OD∥AE…（5分）

又∵DE⊥AE，∴DE⊥OD

∵OD是⊙O的半径

∴DE是⊙O的切线．…（10分）

解析

证明：连接OD，

∵OA=OD，∴∠ODA=∠OAD

∵∠BAC的平分线是AD

∴∠OAD=∠DAC

∴∠DAC=∠ODA，可得OD∥AE…（5分）

又∵DE⊥AE，∴DE⊥OD

∵OD是⊙O的半径

∴DE是⊙O的切线．…（10分）

1

题型：填空题

|

填空题

（几何证明选讲选做题）已知PA是圆O（O为圆心）的切线，切点为A，PO交圆O于B，C两点，AC=，∠PAB=30°，则圆O的面积为______．

正确答案

解析

解：已知如图：

∵PA是圆O（O为圆心）的切线，，∠PAB=30°，

由弦切角定理得∠C=30°

又∵BC为直径，

∴∠BAC=90°

又∵AC=，

∴2R=BC=，即R=

则圆O的面积为S==

故答案为：

1

题型：填空题

|

填空题

如图，在△ABC中，AB=AC，∠C=72°，⊙O过A、B两点且与BC相切于点B，与AC交于点D，连接BD，若BC=，则AC=______．

正确答案

2

解析

解：∵AB=AC，∠C=72°

∴∠A=36°

圆O过AB两点且BC切于B

∴∠CBD=∠A=36°

∴∠ABD=36°

∴AD=BD

∠BDC=72°

BC=BD

∴△ABC∽△BCD

∴BC 2=CD•AC=（AC-BC）AC

∴AC=2

故答案为：2

1

题型：填空题

|

填空题

如图，已知圆中两条弦AB与CD相交与F，且DF=CF=，E是AB延长线上一点，AF：FB：BE=4：2：1，若CE与圆相切，则线段CE的长为______．

正确答案

解析

解：设AF=4k，BF=2k，BE=k，由DF•FC=AF•BF，得2=8k2，即k=，

∴AF=2，BF=1，BE=，AE=，

由切割定理得CE2=BE•EA==

∴CE=．

故答案为：．

1

题型：单选题

|

单选题

如图，AB是的直径，PB，PE分别切⊙O于B，C，∠ACE=40°，则∠P=（　　）

A60°

B70°

C80°

D90°

正确答案

C

解析

解：连接BC，

∵AB是⊙O的直径

∴∠ACB=90°，

又∠ACE=40°，且PB=PC

∴∠PCB=∠PBC=50°，

∴∠P=180°-50°-50°=80°

故选：C．

1

题型：填空题

|

填空题

如图所示，DB，DC是⊙O的两条切线，A是圆上一点，已知∠D=46°，则∠A=______．

正确答案

67°

解析

解：由圆的切线的性质可知，DB=DC

∵∠D=46°

∴∠DBC=∠DCB=67°

∵DB，DC是⊙O的两条切线

∴∠DBC是圆的弦切角，且A是圆的圆周角

由弦切角定理可知，∠DBC=∠A=67°

故答案为67°

1

题型：填空题

|

填空题

如图，AB是⊙O的直径，BC是⊙O的切线，AC与⊙O交于点D，若BC=3，，则AB的长为______．

正确答案

4

解析

解：∵BC是⊙O的切线，∴BC2=CD•CA，即，CD＞0，解得CD=．

∴AC=5．

由BC是⊙O的切线，∴AB⊥BC．由勾股定理可得==4．

故答案为4．

1

题型：简答题

|

简答题

选修4-1：几何证明选讲：

如图，AB为⊙O的直径，D为⊙O上一点且CD⊥AB于C，E，F分别为圆上的点满足∠ACF=∠BCE，直线FE、AB交于P，求证：PD为⊙O的切线．

正确答案

证明：延长FC交圆与G，连接GB、OD，如图．

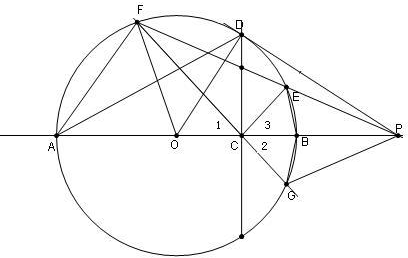
∠POF=2∠OAF，

而∠PEC=∠PEB+∠BEC=∠PAF+∠BGC=∠PAF+∠PAF=2∠PAF，

∴∠POF=∠PEC

又根据圆的对称性，得∠PGC=∠PEC

在△PGC和△FOC中，∠1=∠2，

∠PGC=∠PEC，

∴△PGC∽△FOC，

∴PC•OC=GC•FC，

又CD2=GC•FC，

∴PC•OC=CD2

∴△PDC∽△DOC．

∴∠PDC=∠DOC，

∵∠DOC+∠ODC=90°，

∴∠PDC+∠ODC=90°，

∴PD是⊙O的切线．

解析

证明：延长FC交圆与G，连接GB、OD，如图．

∠POF=2∠OAF，

而∠PEC=∠PEB+∠BEC=∠PAF+∠BGC=∠PAF+∠PAF=2∠PAF，

∴∠POF=∠PEC

又根据圆的对称性，得∠PGC=∠PEC

在△PGC和△FOC中，∠1=∠2，

∠PGC=∠PEC，

∴△PGC∽△FOC，

∴PC•OC=GC•FC，

又CD2=GC•FC，

∴PC•OC=CD2

∴△PDC∽△DOC．

∴∠PDC=∠DOC，

∵∠DOC+∠ODC=90°，

∴∠PDC+∠ODC=90°，

∴PD是⊙O的切线．

1

题型：填空题

|

填空题

如图，△ABC是圆的内接三角形，PA切圆于点A，PB交圆于点D．若∠ABC=60°，PD=1，BD=8，则∠PAC=______°，PA=______．

正确答案

60

3

解析

解：∵PD=1，BD=8，

∴PB=PD+BD=9

由切割线定理得PA2=PD•PB=9

∴PA=3

又∵PE=PA

∴PE=3

又∠PAC=∠ABC=60°

故答案：60，3

1

题型：填空题

|

填空题

如图，△ABC内接于⊙O，过BC中点D作平行于AC的直线l，l交AB于E，交⊙O于G、F，交⊙O在A点的切线于P，若PE=3，ED=2，EF=3，则PA的长为______．

正确答案

解析

解：∵D是BC的中点，DE∥AC，∴AE=BE，且∠BDE=∠C．

又∵PA切圆O于点A，∴∠PAE=∠C，可得∠BDE=∠PAE．

∵∠BED=∠PEA，

∴△BED∽△PEA，可得，

∴AE2=BE•AE=PE•ED=6．

由此解出AE=．

∵AE2=GE•EF，∴GE=2，

∴PG=1，

∴PA2=PG•PF=6，

∴PA=．

故答案为：．

1

题型：简答题

|

简答题

如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．

（Ⅰ）求证：AC是△BDE的外接圆的切线；

（Ⅱ）若AD=2，AE=6，求EC的长．

正确答案

证明：（Ⅰ）取BD的中点O，连接OE．

∵BE平分∠ABC，∴∠CBE=∠OBE．又∵OB=OE，∴∠OBE=∠BEO，

∴∠CBE=∠BEO，∴BC∥OE．…（3分）

∵∠C=90°，∴OE⊥AC，∴AC是△BDE的外接圆的切线． …（5分）

（Ⅱ）设⊙O的半径为r，则在△AOE中，OA2=OE2+AE2，即，

解得，…（7分）

∴OA=2OE，

∴∠A=30°，∠AOE=60°．

∴∠CBE=∠OBE=30°．

∴在Rt△BCE中，可得EC=． …（10分）

解析

证明：（Ⅰ）取BD的中点O，连接OE．

∵BE平分∠ABC，∴∠CBE=∠OBE．又∵OB=OE，∴∠OBE=∠BEO，

∴∠CBE=∠BEO，∴BC∥OE．…（3分）

∵∠C=90°，∴OE⊥AC，∴AC是△BDE的外接圆的切线． …（5分）

（Ⅱ）设⊙O的半径为r，则在△AOE中，OA2=OE2+AE2，即，

解得，…（7分）

∴OA=2OE，

∴∠A=30°，∠AOE=60°．

∴∠CBE=∠OBE=30°．

∴在Rt△BCE中，可得EC=． …（10分）

1

题型：填空题

|

填空题

如图，已知PA是圆O的切线，切点为A，直线PO交圆O于B，C两点，AC=1，∠BAP=120°，则圆O的面积为______．

正确答案

π

解析

解：∵PA是圆O的切线，

∴OA⊥AP．

又∵∠PAB=120°，

∴∠BAO=∠ABO=30°．

又∵在Rt△ABC中，AC=1，

∴BC=2，即圆O的直径2R=2，

∴圆O的面积S=πR2=π，

故答案为：π．

1

题型：简答题

|

简答题

圆的两条弦AB、CD交于点F，从F点引BC的平行线和直线DA的延长线交于点P，再从点P引这个圆的切线，切点是Q．求证：PF=PQ．

正确答案

解：∵ABCD四点共线

∴∠ADF=∠ABC

又∵PF∥BC

∴∠AFP=∠FDP

又∵∠CPF=∠FPD

∴△APF∽△FPD

∴

∴PF2=PA•PD

又PQ与圆相切

∴PQ2=PA•PD

∴QF2=PQ2

∴PF=PQ

解析

解：∵ABCD四点共线

∴∠ADF=∠ABC

又∵PF∥BC

∴∠AFP=∠FDP

又∵∠CPF=∠FPD

∴△APF∽△FPD

∴

∴PF2=PA•PD

又PQ与圆相切

∴PQ2=PA•PD

∴QF2=PQ2

∴PF=PQ

热门试卷

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析

正确答案

解析