- 元素与集合关系的判断
- 共59题
已知集合


正确答案

解析
由集合的并集意义得
知识点
已知全集为


正确答案
解析
略
知识点
设















正确答案
解析
略
知识点
设





(1)当

(2)证明:对任意集合


(3)设



正确答案
见解析
解析
(1)当

………4分
(2)设集合

所以



所以


设集合

所以


所以


所以
所以
(3)假设
因为

所以

由假设可知,每个元素的元素数值和都不相等,
所以
这与“元素的数值和
所以假设错误。
所以
知识点
已知集合

正确答案
解析
略
知识点
下列命题中,真命题是
正确答案
解析
略
知识点
用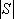
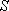
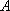
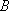
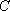
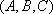
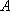
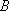
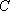

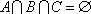
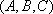
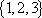
正确答案
6
解析
略
知识点
设集合



①




(1)求
(2)求

正确答案
(1)4;(2)
解析
(1)当


∴ 
( 2 )任取偶数






由条件知,若



于是



设



当



∴
知识点
设集合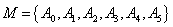
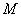
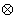
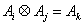
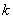
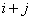
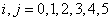
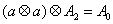
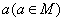
正确答案
解析
设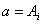
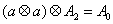
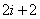
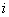
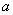
知识点
已知全集U=Z,A={0,1,2,3},B={x|x2=2x},则A∩
正确答案
解析
略
知识点
扫码查看完整答案与解析