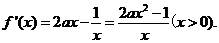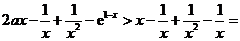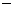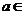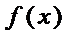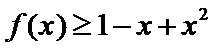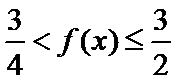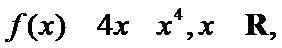- 利用导数求参数的取值范围
- 共134题
20.设f(x)=xlnx–ax2+(2a–1)x,a∈R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
正确答案
(Ⅰ)当


当



(Ⅱ) 
解析
试题分析:(Ⅰ)求导数
可得
从而
讨论当

(Ⅱ)由(Ⅰ)知,




试题解析:(Ⅰ)由
可得
则
当



当






所以当


当



(Ⅱ)由(Ⅰ)知,
①当


所以当


当


所以
②当



可得当当



所以

所以
③当



所以当


④当




当


所以f(x)在x=1处取得极大值,合题意.
综上可知,实数a的取值范围为
考查方向
知识点
已知函数
(I)当


(II)若当


正确答案
(I)






(II)当

令

(i)当





(ii)当


由







综上,
知识点
设函数f(x)=ax2-a-lnx,g(x)=-,其中a∈R,e=2.718…为自然对数的底数。
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)证明:当x>1时,g(x)>0;
(Ⅲ)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立。
正确答案
(I)
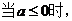
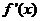
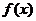
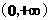
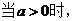
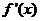
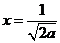
当

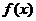
当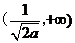
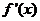

(II)令
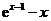
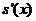

当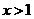

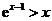
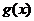
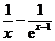
(iii)由(II),当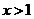
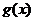
当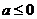
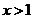
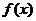
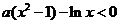
故当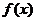

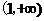
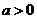
当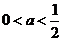
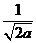
由(I)有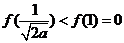
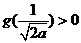
所以此时
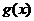
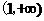
当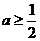
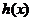
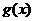
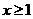
当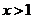
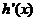
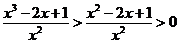
因此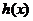
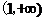
又因为
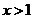
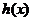
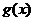
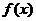
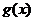
综上,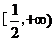
知识点
设函数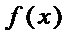
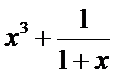
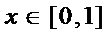
24.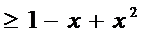
25.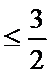
正确答案
证明详见解析
解析
(Ⅰ)因为
由于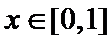
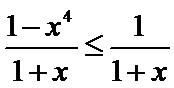
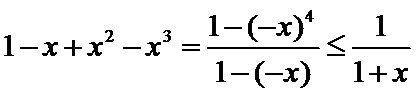
所以
考查方向
解题思路
利用放缩法,得到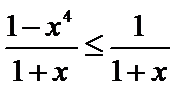
易错点
对函数的单调性与最值、分段函数等基础知识不熟悉,计算错误
正确答案
证明详见解析.
解析
由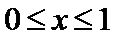
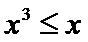
故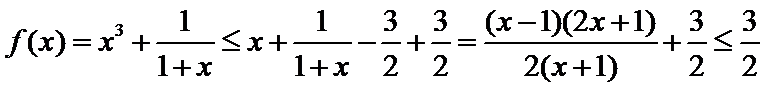
所以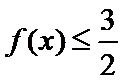
由(Ⅰ)得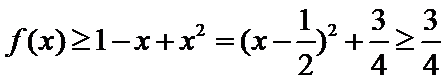
又因为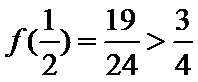
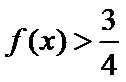
综上,
考查方向
解题思路
由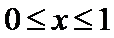
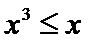
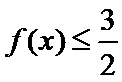
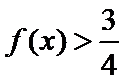
易错点
对函数的单调性与最值、分段函数等基础知识不熟悉,计算错误
已知函数
26.求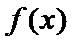
27.设曲线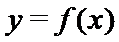
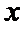
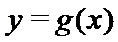
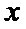
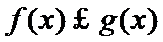
28.若方程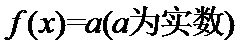
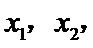
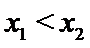
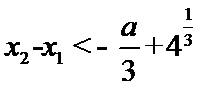
正确答案
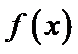
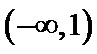
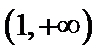
解析
试题分析:由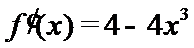
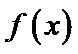
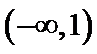
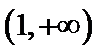
由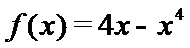
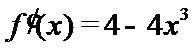
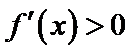
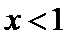
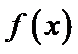
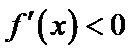
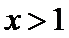
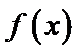
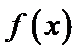
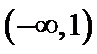
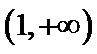
考查方向
解题思路
给出可导函数求单调区间,实质是解关于导函数的不等式,若函数解析式中不含参数,一般比较容易.不过要注意求单调区间,要注意定义域优先原则,且结果必须写成区间形式,不能写成不等式形式.
易错点
导数函数性质与原函数单调性的关系.
正确答案
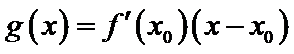
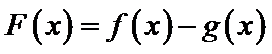
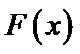
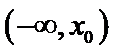
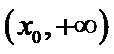
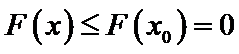
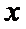
设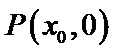
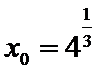
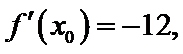
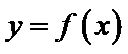
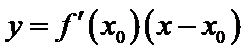
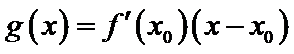
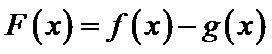
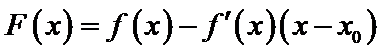
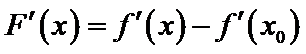
由于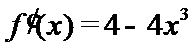
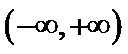
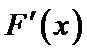
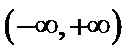
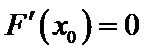
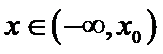
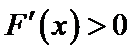
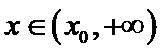
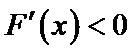
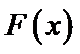
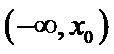
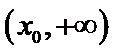
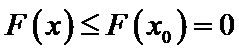
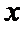
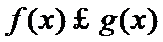
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
构造函数的性质与所求问题的联系
正确答案
设方程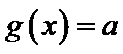
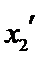
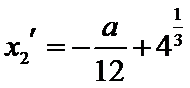
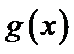
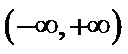
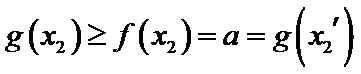
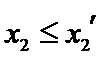
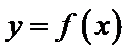
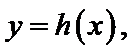
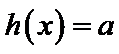
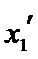
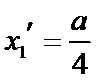
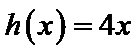
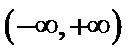
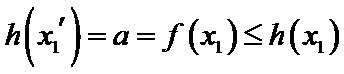
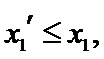
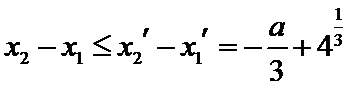
由(II)知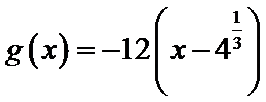
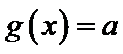
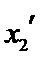
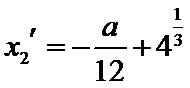
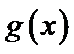
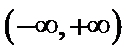
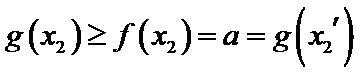
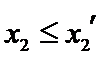
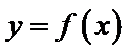
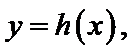
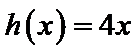
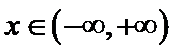
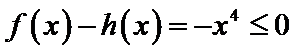
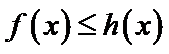
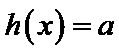
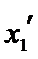
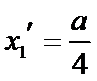
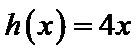
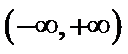
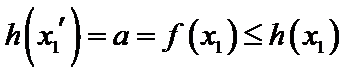
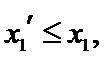
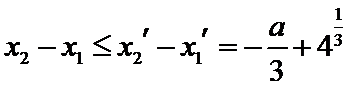
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
导数的几何意义及导函数与原函数之间的联系
扫码查看完整答案与解析