- 利用导数求参数的取值范围
- 共134题
已知曲线
(1)求曲线在点(
(2)若存在实数


正确答案
(1)y=(a-1)x-1
(2)
解析
(1)因为


所以曲线在点(
(2)因为a>0,由








因为存在



知识点
已知函数

(1)讨论函数
(2)若函数




正确答案
见解析
解析
(1)在区间

①若



②若


在区间


在区间


综上所述,①当


②当



(2)因为函数

解得
由已知

令

易得


所以

知识点
已知三次函数



(1)求
(2)若当且仅当


正确答案
见解析。
解析
(1)




(2)令
则
因为

所以

故


知识点
已知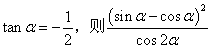
正确答案
解析
略
知识点
已知三次函数


(1)求函数
(2)若函数
正确答案
见解析。
解析
(1)




令
则
因为



故


(2)


①当




②当




③当


由



故在

所以当


当


当



故

知识点
扫码查看完整答案与解析