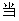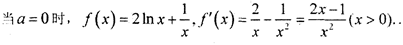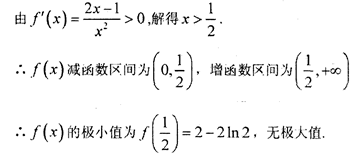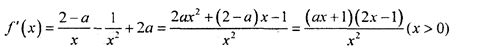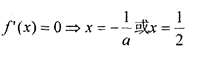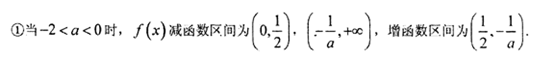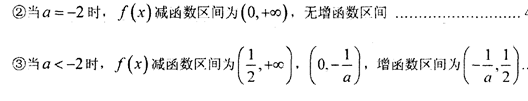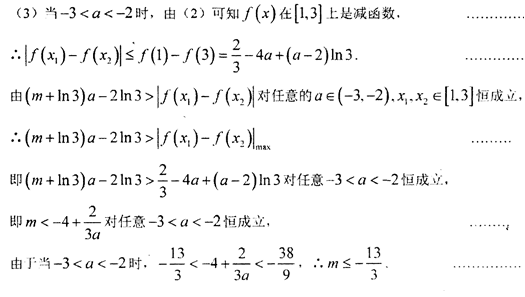- 利用导数求参数的取值范围
- 共134题
已知函数

(1)求实数
(2)若关于



正确答案
见解析。
解析
(1)
∵


故

经检验

(2)









当



当



依题意有
解得
∴实数

知识点
已知函数




(1)求函数
(2)若曲线


正确答案
见解析。
解析
(1)
依题意

∴
(2)由(1)知,曲线

交点,即

设

由

当



当



依题意有
∴实数

知识点
已知函数
(1)若

(2)若

正确答案
见解析。
解析
(1)若


∵



∴
(2)要使


显然当


∴
当


当



①当



∴

②当



∴

③当





∴
∵


由①②③可得
知识点
已知函数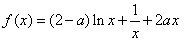
(1)当
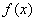
(2)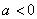
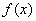
(3)若对任意的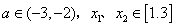
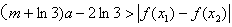
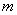
正确答案
见解析。
解析
(1)解:
(2)
知识点
设函数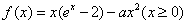
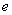
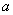
(1)若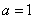
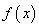
(2)当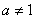
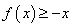
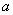
正确答案
见解析。
解析
解:
知识点
扫码查看完整答案与解析