- 利用导数求参数的取值范围
- 共134题
已知函数
(1)当a=1时,∃x0∈[1,e]使不等式f(x0)≤m,求实数m的取值范围;
(2)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,求实数a的取值范围。
正确答案
见解析。
解析
(1)当a=1时,
可知当x∈[1,e]时f(x)为增函数,
最小值为
要使∃x0∈[1,e]使不等式f(x0)≤m,即f(x)的最小值小于等于m,
故实数m的取值范围是
(2)已知函数
若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax的下方,
等价于对任意x∈(1,+∞),f(x)<2ax,
即
设
即g(x)的最大值小于0.
(1)当

∴
∴g(1)=﹣a﹣
∴a≥﹣
∴
(2)a≥1时,

g(x)无最大值,即最大值可无穷大,故此时不满足条件。
(3)当


同样最大值可无穷大,不满足题意,综上,实数a的取值范围是
知识点
若
正确答案
解析
略
知识点
设

(1)若


(2)若函数


正确答案
见解析
解析
(1)
因为



所以



即
(2)由题设,

所以,

这等价于,不等式

令

则
所以

所以

所以


知识点
设函数
(1)若



(2)若

正确答案
见解析。
解析
(1)



又





由

又




(2)若






化为



知识点
已知函数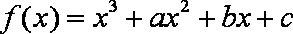
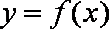
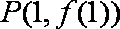
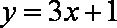
(1)若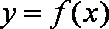
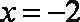
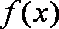
(2)若函数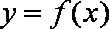
正确答案
见解析。
解析
(1)由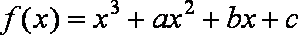
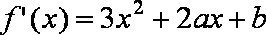
过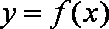
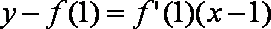
即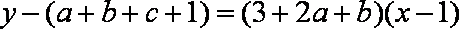
而过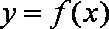
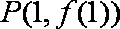
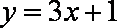
故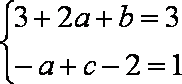
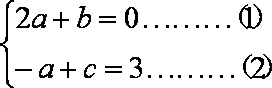
因为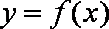
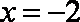
故
由(1)(2)(3)联立解得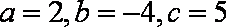
所以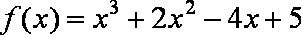
(2)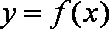
又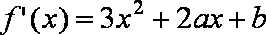
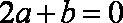
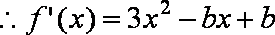
依题意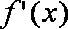
即
①在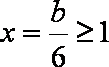
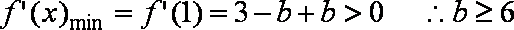
②在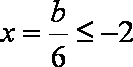
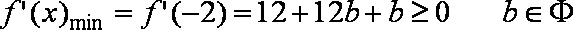
③在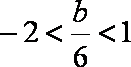
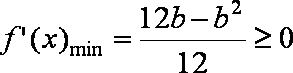
综合上述讨论可知,所求参数b的取值范围是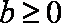
知识点
扫码查看完整答案与解析