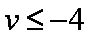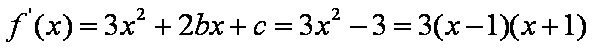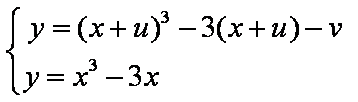- 利用导数求参数的取值范围
- 共134题
已知函数f(x)=lnx﹣x,
(1)求h(x)的最大值;
(2)若关于x的不等式xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,求实数a的取值范围;
(3)若关于x的方程f(x)﹣x3+2ex2﹣bx=0恰有一解,其中e是自然对数的底数,求实数b的值。
正确答案
见解析。
解析
(1)因为

由h′(x)>0,且x>0,得0<x<e,由h′(x)<0,且x>0,x>e,
所以函数h(x)的单调增区间是(0,e],单调减区间是[e,+∞),
所以当x=e时,h(x)取得最大值
(2)因为xf(x)≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,
即xlnx﹣x2≥﹣2x2+ax﹣12对一切x∈(0,+∞)恒成立,
亦即
设

故ϕ(x)在(0,3]上递减,在[3,+∞)上递增,ϕ(x)min=ϕ(3)=7+ln3,
所以a≤7+ln3.
(3)因为方程f(x)﹣x3+2ex2﹣bx=0恰有一解,
即lnx﹣x﹣x3+2ex2﹣bx=0恰有一解,即
由(1)知,h(x)在x=e时,
而函数k(x)=x2﹣2ex+b+1在(0,e]上单调递减,在[e,+∞)上单调递增,
故x=e时,k(x)min=b+1﹣e2,
故方程

即b=e2+
知识点
角




正确答案
解析
略
知识点
如图,已知C是以AB为直径的元O上一点,
(1)求证:CG是元O的切线
(2)若
正确答案
见解析
解析
解析:
(1)证明:连接CB、OC,
∵CH⊥AB,DB⊥AB,∴CH // BD,
∴
∵AB是直径,∴∠ACB=90°∴∠BCD=90°
在Rt△BCD中
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∵∠ACB=90°∴∠OCF=90°,∴CG是⊙O的切线.
(2)由FC=FB=FE得:∠FCE=∠FEC,

得:
由切割线定理得:(2+FG)2=BG×AG=2BG2 ……①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ……②
由①、②得:FG2-4FG-12=0,解之得:FG=6或FG=-2(舍去)
∴AB=BG=

知识点
已知函数
(1)若

(2)若


正确答案
见解析
解析
(1)当













(2)由







令




∴
即


知识点
若函数


(1)函数
(2)已知函数


正确答案
见解析
解析
(1)函数
则定义域内存在实数

构造函数

∵



∴

即存在

另解:函数
由

即
作函数

由图象可以看出,存在

即
(2)

由已知,存在

即
整理,得

∴

由


∴a的取值范围是
知识点
已知函数
(1)若函数

(2)若对任意给定的
使得
正确答案
见解析。
解析
(1)因为



令












(2)







当
当







此时,当
又因为,当








令













综合①④可知,当
在

知识点
已知函数
(1)证明:

(2)若关于x的不等式

(3)已知正数a满足:存在



正确答案
见解析。
解析
(1)



(2)由题意,
∵



令


∵

∴
(3)




令
∵



∵存在


∵
设
当


当


因此
∴当


当


当


知识点
如图, ⊙O为










求证:(1)
(2)点



正确答案
见解析。
解析
(1)∵直线

∵


∴

又∵

∴

∴
∴
(2)由(1)可知
∵

∴

∴点



知识点
已知函数
(1)若


(2)若

正确答案
(1)
(2)
解析
(1)由


所以

所以所求切线方程为
即
(2)由已知

因为函数

即不等式

令

当


当


由此得


知识点
已知函数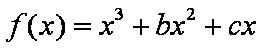
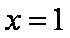
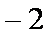
(1)求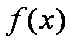
(2)若对任意的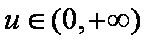
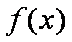

正确答案
(1)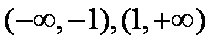
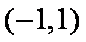
(2)
解析
(1)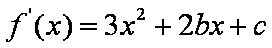
由题意得: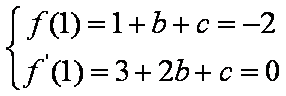
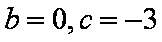
∴
∴当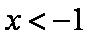
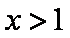

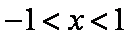
∴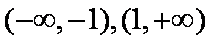
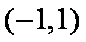
(2)
由方程组
得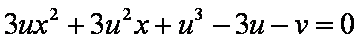
∴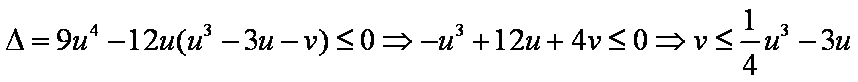
……………………………………9 分
令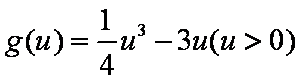
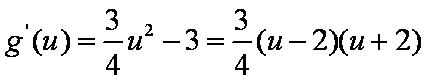
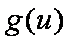
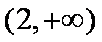
所以当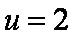
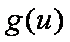
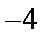
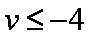
知识点
扫码查看完整答案与解析