- 利用导数求参数的取值范围
- 共134题
8.已知函数f(x)=x2+mx+ln x是单调递增函数,则m的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设
(1)若


(2)若


正确答案
(1)-5
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数


(1)若

(2)若直线




(3)若在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)若

(2)若函数



(3)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)当
(2)若函数
(3)若对于任意的

正确答案
解:(1)
当
令
当

所以
在区间
(2)

则方程

这时,
因此满足条件的
(3)由(2)知,当
当
因此函数
又
于是
因此满足条件的
解析
解析已在路上飞奔,马上就到!
知识点
22.已知
(1)当AB边通过坐标原点O时,求AB的长及
(2)当
正确答案
(1)因为
所以AB所在直线的方程为
由
A(1,1),B(-1,-1)。
又
(2)设AB所在直线的方程为
由
因为A,B两点在椭圆上,
所以
设A,B两点坐标分别为

又


所以,AB所在直线的方程为
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若


(2)求
(3)设




正确答案
(1)由已知

故曲线


(2)
①当


所以,

②当


在区间



所以,函数


(3)由已知,转化为
由(2)知,当



(或者举出反例:存在
当



故

所以
解得
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)讨论
(Ⅱ)若

(Ⅲ)设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数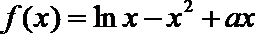
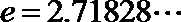
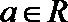
(Ⅰ)当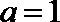
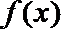
(Ⅱ)若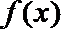
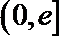
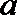
(Ⅲ)设函数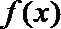
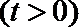
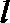
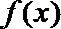
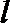
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在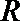
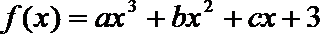
① 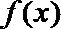
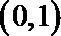
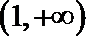
② 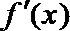
③ 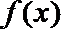
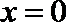
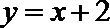
(1)求函数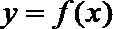
(2)设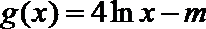
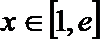
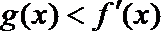
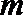
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析