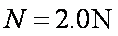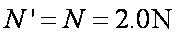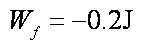- 机械能
- 共1183题
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)在满足(1)的条件下,小球在最高点P突然离开轻杆沿水平方向飞出,试求小球落到水平轨道位置到轴O的距离;
(3)若解除对滑块的锁定,小球通过最高点时的速度大小v′=2m/s,试求此时滑块的速度大小。
正确答案
(1)小球对轻杆的作用力大小为2N,方向竖直向上
(2)
(3)v =1m/s
解析
(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则
得
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则
得F=2N
由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上
(2)小球飞出后做平抛运动,设运动时间为t
由
到轴O的距离
得
(3)解除锁定后,设小球通过最高点时的速度为v2。
在上升过程中,系统的机械能守恒,则
得v =1m/s
知识点
如图所示,质量m的小物块从高为h的坡面顶端由静止释放,滑到粗糙的水平台上,滑行距离l后,以v = 1 m/s的速度从边缘O点水平抛出,击中平台右下侧挡板上的P点,以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板形状满足方程 
(1)小物块在水平台上滑行的距离l ;
(2)P点的坐标。
正确答案
(1)
(2)(1m, -5m)
解析
(1)对小物块,从释放到O点过程中
解得
(2) 小物块从O点水平抛出后满足


由①②解得小物块的轨迹方程
又有
由③ ④ 得x =1m, y = -5m⑤
所以P点坐标为(1m, -5m)⑥
知识点
如图11所示,在一竖直平面内,BCDF段是半径为R的圆弧挡板,AB段为直线型挡板(长为4R),两者在B点相切,

正确答案
解析
略
知识点
光滑圆轨道和两倾斜直轨道组成如图所示装置,其中直轨道bc粗糙,直轨道cd光滑,两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块(可视为质点)在圆轨道上做圆周运动,到达轨道最高点a时的速度大小为v=4m/s,当滑块运动到圆轨道与直轨道bc的相切处b时,脱离圆轨道开始沿倾斜直轨道bc滑行,到达轨道cd上的d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计,已知圆轨道的半径为R=0.25m,直轨道bc的倾角
(1)滑块在圆轨道最高点a时对轨道的压力大小;
(2)滑块与直轨道bc问的动摩擦因数;
(3)滑块在直轨道bc上能够运动的时间。
正确答案
(1)5.4N
(2)0.8
(3)7.66s
解析
(1)在圆轨道最高点a处对滑块由牛顿第二定律得:
∴
由牛顿第三定律得滑块在圆轨道最高点a时对轨道的压力大小为5.4N
(2) 从a点到d点全程由动能定理得:

(3)设滑块在bc上向下滑动的加速度为a1,时间为t1,向上滑动的加速度为a2,时间为t2;在c点时的速度为vc。
由c到d:

a点到b点的过程:
∴
在轨道bc上:
下滑:

上滑:


∵
滑块在两个斜面上运动的总时间:

知识点
如图所示,一物体m在沿斜面向上的恒力F作用下,由静止从底端沿光滑的斜面向上做匀加速直线运动,经时间t力F做功为60J,此后撤去恒力F,物体又经t时间回到出发点,(取g=10m/s2),若以地面为零势能点,则下列说法正确的是( )
正确答案
解析
略
知识点
光滑水平面上有一边长为l的正方形区域,处在电场强度为E的匀强电场中,电场方向与正方形的某一边平行。一质量为m、带电荷量为+q的小球由某一边的中点,以垂直于该边的水平初速度进入该正方形区域。当小球再次运动到该正方形区域的边缘时,动能的增量不可能为C
正确答案
解析
略
知识点
如图所示,在外力作用下某质点运动的速度v-时间t图像为正弦曲线,由图可判断( )
正确答案
解析
略
知识点
如图所示,半径为R的光滑圆环竖直放置,环上套有质量分别为m和2m的小球A和B,A、B之间用一长为
正确答案
解析
略
知识点
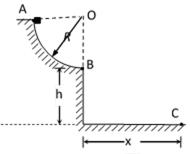
在竖直平面内有一个粗糙的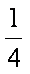
求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
正确答案
见解析。
解析
(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,则
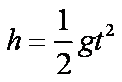
解得: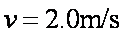
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N,根据牛顿第二定律: 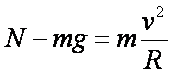
解得:
根据牛顿第三定律,轨道受到的压力大小
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
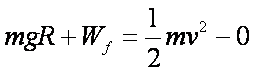
所以小滑块克服摩擦力做功为0.2J。
知识点
2012年9月25日,中国航母“辽宁舰”正式交付海军,这将极大提高我们中国海军的整体作战实力。如图所示是“歼—15飞机”在航母“辽宁舰”上的起降示意图。已知“歼—15飞机”的质量为m,它的发动机额定功率恒定,起飞前在航母上运动过程中所受的摩擦阻力为恒力。“歼—15飞机”以额定功率从静止开始沿航母做直线运动,到航母一端后起飞。设“歼—15飞机”经过时间t运动了位移s时,速度达到最大值v,此时刚好离开航母起飞。则“歼—15飞机”发动机在航母上运动过程所做的功为
正确答案
解析
略
知识点
扫码查看完整答案与解析