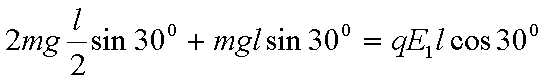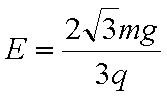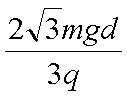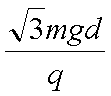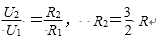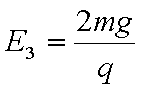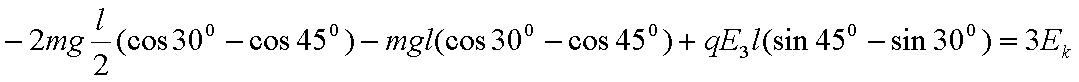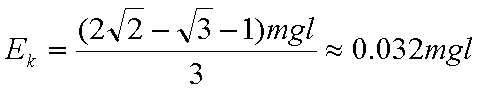- 机械能
- 共1183题
22. 一质量为0.5kg的小物块放在水平地面上的A点。距离A点5m的位置处事一面墙,如图所示。物块以v0=9m/s的初速度从A点沿AB方向运动过,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止。g取10m/s。
(1)求物块与地面间的动摩擦因数μ;
(2)若碰撞时间为0.05s,求碰撞过程中墙面对物块平均作用力的大小F;
(3)求物块在反向运动过程中客服摩擦力所做的功W。
正确答案
解:(1)由动能定理,
有
可得
(2)由动量定理,有
可得
(3)
解析
解析已在路上飞奔,马上就到!
知识点
如图,一对很大的竖直放置的平行金属板可以绕M、N左右转动,其之间存在一水平匀强电场。有一长为l的轻质细绝缘棒OA处于电场中,其一端可绕O点在竖直平面内自由转动,另一端A处固定一带电-q、质量为m的小球a,质量为2m的绝缘不带电小球b固定在OA棒中点处。滑动变阻器电阻足够大,当变阻器滑片在P点处时,棒静止在与竖直方向成30°角的位置,已知此时BP段的电阻为R,M、N两点间的距离为d。试求:(重力加速度为g)
(1)求此时金属板间电场的场强大小E;
(2)若金属板顺时针旋转α=30°(图中虚线表示),并移动滑片位置,欲使棒静止在与竖直方向成30°角的位置,BP段的电阻应调节为多大?
(3)若金属板不转动,将BP段的电阻突然调节为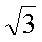
正确答案
见解析
解析
(1)小球和棒力矩平衡:
金属板间电场的场强大小
(2)金属板间电势差U1=E1d=
金属板旋转30°后平衡,
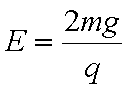
金属板间电势差与变阻器BP电阻成正比,因此
(3)BP段的电阻调节为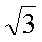
设小球动能最大时,细线与竖直角度为θ,即摆动过程中的平衡位置,根据力矩平衡得到: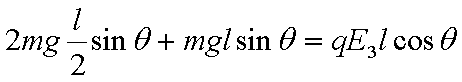
a的速度是b的2倍,a的质量是b的一半,所以a的动能是 b的动能2倍,设b的最大动能为Ek,对整体,根据动能定理得到:
解得:
知识点
26.如图所示,在绝缘水平面上的P点放置一个质量为




(1)A经过多少时间与B相碰?相碰结合后的速度是多少?
(2)AB与墙壁碰撞后在水平面上滑行的过程中,离开墙壁的最大距离是多少?
(3)A.B相碰结合后的运动过程中,由于摩擦而产生的热是多少?通过的总路程是多少?
正确答案
(1)由于PQ部分光滑,滑块A只在电场力作用下加速运动
设经时间t与B相碰,A与B相遇前的速度大小为

则

解得t=0.3m / s ,
滑块A.B碰撞的过程中动量守恒,即
(2)两滑块共同运动,与墙壁发生碰撞后返回,第一次速度为零时,两滑块离开墙壁的距离最大,设为

(3)由于

设由于摩擦而产生的热为Q,由能量守恒得
设AB第二次与墙壁发生碰撞后返回,滑块离开墙壁的最大距离为



设在粗糙水平面OQ部分运动的总路程


设AB相碰结合后的运动过程中通过的总路程是

解析
解析已在路上飞奔,马上就到!
知识点
24.如图所示,在倾角为30°的光滑斜面上,有一劲度系数为k的轻质弹簧,其一端固定在固定挡板C上,另一端连接一质量为m的物体A.有一细绳通过定滑轮,细绳的一端系在物体A上(细绳与斜面平行),另一端系有一细绳套,物体A处于静止状态.当在细绳套上轻轻挂上一个质量为m的物体B后,物体A将沿斜面向上运动,试求:
(1)未挂物体B时,弹簧的形变量;
(2)物体A的最大速度值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.升降机底板上放一质量为100 kg的物体,物体随升降机由静止开始竖直向上移动5m时速度达到4m/s,g取10m/s2,则此过程中( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,一个电量为+Q的点电荷甲,固定在绝缘水平面上的O点,另一个电量为-q、质量为m的点电荷乙从A点以初速度v0沿它们的连线向甲运动,到B点时速度最小且为v,已知静电力常量为k,点电荷乙与水平面的动摩擦因数为μ,AB间距离为L,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25. 如图所示,一块小磁铁放在铁板ABC的A处,其中AB长1m,BC长0.8m,BC与水平面间的夹角为37°,小磁铁与铁板间的引力为磁铁重的0.2倍,小磁铁与铁板间的动摩擦因数μ=0.25,现在给小磁铁一个水平向左的初速度v0=4m/s。不计磁铁经过B处的机械能损失,取g=10m/s2,已知sin37°=0.6,cos37°=0.8。则:
(1)小磁铁第一次到达B处的速度大小;
(2)小磁铁在BC段向上运动时的加速度大小;
(3)请分析判断小磁铁能否第二次到达B处。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.我人民海军进行登陆演练,假设一艘战舰因吨位大,吃水太深,只能停在离海岸某处。登陆队员需要利用绳索,从较高的军舰甲板滑到登陆快艇上,再接近目标。若绳索两端固定好后,与竖直方向的夹角θ=30°,队员甲先匀加速滑到最大速度,再靠摩擦匀减速滑至快艇,速度刚好为零;当队员甲开始下滑的同时,队员乙在甲板上的相同位置,向快艇以速度v0=
(1)军舰甲板到快艇的竖直高度H;
(2)队员甲在绳索上运动的时间t0及下滑过程中的最大速度v1;
(3)已知快艇的额定功率P=5kw,载人后连同装备总质量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,

(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物块与斜面间的动摩擦因数
(3)若小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.如图甲所示,“
(1)斜面BC的长度;
(2)滑块的质量;
(3)运动过程中滑块克服摩擦力做的功。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析