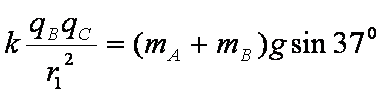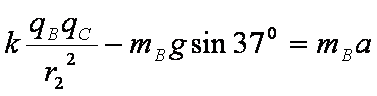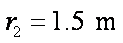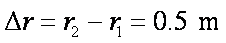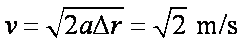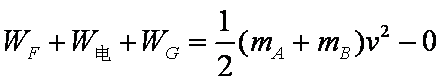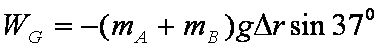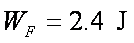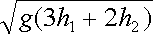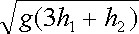- 机械能
- 共1183题
33.如图(a),磁铁A、B的同名磁极相对放置,置于水平气垫导轨上.A固定于导轨左端,B的质量m=0.5kg,可在导轨上无摩擦滑动.将B在A附近某一位置由静止释放,由于能量守恒,可通过测量B在不同位置处的速度,得到B的势能随位置x的变化规律,见图(c)中曲线I。若将导轨右端抬高,使其与水平面成一定角度(如图(b)所示),则B的总势能曲线如图(c)中II所示,将B在x=20.0cm处由静止释放,求:(解答时必须写出必要的推断说明。取g=9.8 m/s2)
(1)B在运动过程中动能最大的位置;
(2)运动过程中B的最大速度和最大位移;
(3)图(c)中直线III为曲线II的渐近线,求导轨的倾角;
(4)若A、B异名磁极相对放置,导轨的倾角不变,在图(c)上画出B的总势能随x的变化曲线。
正确答案
见解析。
解析
(1)势能最小处动能最大
由图线II得
(在5.9 ~ 6.3cm间均视为正确)
(2)由图读得释放处势能

(
最大速度为
(
x=20.0 cm处的总能量为0.90J,最大位移由E=0.90J的水平直线与曲线II的左侧交点确定,由图中读出交点位置为x=2.0cm,因此,最大位移
(
(3)渐近线III表示B的重力势能随位置变化关系,即

∴
由图读出直线斜率
(

(4)若异名磁极相对放置,A,B间相互作用势能为负值,总势能如图。
知识点
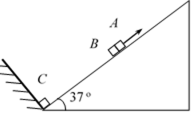
如图所示,可视为质点的物块
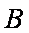
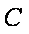
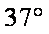
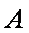
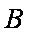
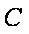
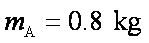
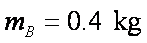
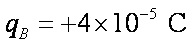

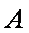
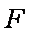
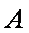
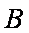
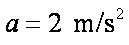
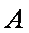
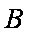
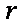
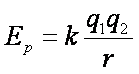
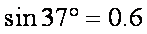
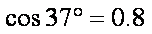
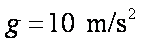
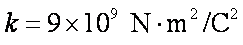
(1)未施加力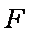
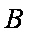
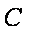
(2)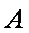
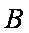
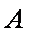
(3)
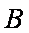
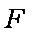
正确答案
见解析。
解析
(1)三物块均静止时,以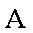
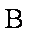
由力的平衡得:
解得:
(2)当
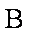
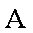
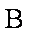
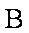
由牛顿第二定律得:
解得
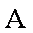
(3)以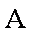
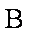
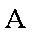
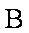
解得:
从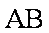
电场力做功为
重力做功为
解得:
知识点
磁悬浮列车是一种高速运载工具,它由两个系统组成。一是悬浮系统,利用磁力使车体在轨道上悬浮起来从而减小阻力。另一是驱动系统,即利用磁场与固定在车体下部的感应金属线圈相互作用,使车体获得牵引力,磁悬浮列车电磁驱动装置的原理示意图如下图所示。即在水平面上有两根很长的平行轨道PQ和MN,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=B。列车底部固定着绕有N匝闭合的矩形金属线圈abcd(列车的车厢在图中未画出),车厢与线圈绝缘。两轨道间距及线圈垂直轨道的ab边长均为L,两磁场的宽度均与线圈的ad边长相同。当两磁场Bl和B2同时沿轨道方向向右运动时,线圈会受到向右的磁场力,带动列车沿导轨运动。已知列车车厢及线圈的总质量为M,整个线圈的总电阻为R。
(1)假设用两磁场同时水平向右以速度v0作匀速运动来起动列车,为使列车能随磁场运动,列车所受的阻力大小应满足的条件;
(2)设列车所受阻力大小恒为f,假如使列车水平向右以速度v做匀速运动,求为维持列车运动,在单位时间内外界需提供的总能量;
(3)设列车所受阻力大小恒为f,假如用两磁场由静止开始向右做匀加速运动来起动列车,当两磁场运动的时间为t1时,列车正在向右做匀加速直线运动,此时列车的速度为v1,求两磁场开始运动到列车开始运动所需要的时间t0。
正确答案
(1)
(2)
(3)
解析
(1)列车静止时,电流最大,列车受到的电磁驱动力最大设为Fm,此时,线框中产生的感应电动势 E1=2NBLv0
线框中的电流 I1=
整个线框受到的安培力 Fm=2NBI1L
列车所受阻力大小为
(2)当列车以速度v匀速运动时,两磁场水平向右运动的速度为v′,金属框中感应电动势
金属框中感应电流
又因为
求得
当列车匀速运动时,金属框中的热功率为 P1 = I2R
克服阻力的功率为 P2 = fv
所以可求得外界在单位时间内需提供的总能量为
E= I2R +fv=
(3)根据题意分析可得,为实现列车最终沿水平方向做匀加速直线运动,其加速度必须与两磁场由静止开始做匀加速直线运动的加速度相同,设加速度为a,则t1时刻金属线圈中的电动势
金属框中感应电流
又因为安培力
所以对列车,由牛顿第二定律得
解得
设从磁场运动到列车起动需要时间为t0,则t0时刻金属线圈中的电动势
金属框中感应电流
又因为安培力
所以对列车,由牛顿第二定律得
解得
知识点
20.一质量为m的物体在水平恒力F的作用下沿水平面运动,在t0时刻撤去力F,其v-t图像如图所示.已知物体与水平面间的动摩擦因数为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示,传送带足够长,与水平面间的夹角α=37°,并以v=10m/s的速度逆时针匀速转动着,在传送带的A端轻轻地放一个质量为m=1kg的小物体,若已知物体与传送带之间的动摩擦因数μ=0.5,(g=10m/s2,sin37°=0.6,cos37°=0.8)则下列有关说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.图中虚线是用实验方法描绘出的某一静电场中的一簇等势线,若不计重力的带电粒子从a点射入电场后恰能沿图中的实线运动,b点是其运动轨迹上的另一点,则下述判断正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
36.一传送带装置示意如图,传送带在AB区域是倾斜的,倾角θ=30°.工作时传送带向上运行的速度保持v=2m/s不变.现将质量均为m= 2kg的小货箱(可视为质点)一个一个在A处放到传送带上,放置小货箱的时间间隔均为T=1s,放置时初速为零,小货箱一到达B处立即被取走.已知小货箱刚放在A处时,前方相邻的小货箱还处于匀加速运动阶段,此时两者相距为s1=0.5m.传送带装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦,取g=10m/s2。
(1)求小货箱在传送带上做匀加速运动的加速度大小。
(2)AB的长度至少多长才能使小货箱最后的速度能达到v=2m/s?
(3)除了刚释放货箱的时刻,若其它时间内总有4个货箱在传送带上运动,求每运送一个小货箱电动机对外做多少功?并求电动机的平均输出功率
正确答案
(1)小货箱刚放在A处时, 前方相邻的小货箱已经运动了时间T。
有
代入数据解得加速度大小
(2)AB的长度至少为l,则货箱的速度达到v=2m/s时,有
代入数据解得AB的长度至少为l=2m
(3)传送带上总有4个货箱在运动,说明货箱在A处释放后经过t=4T的时间运动至B处。货箱匀加速运动的时间分别是
设货箱受到的滑动摩擦力大小为f,由牛顿定律得
这段时间内,传送带克服该货箱的摩擦力做的功
代入数据解得

代入数据解得
放置小货箱的时间间隔为T,则每隔时间T就有一个小货箱到达B处,因此电动机的平均输出功率
在计算货箱匀加速过程的功时,也可以用以下方式解答:
对货箱,由动能定理得
货箱与传送带发生相对位移产生的热
电动机对传送带做的功
解得:
解析
解析已在路上飞奔,马上就到!
知识点
26.如图14所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2 m 的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动。质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生碰撞,A、B 碰撞前后速度发生交换. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为
(1)求滑块A 从2L高度处由静止开始下滑,与B碰后瞬间B的速度。
(2)若滑块A 能以与球B 碰前瞬间相同的速度与滑块C 相碰,A 至少要从距水平轨道多高的地方开始释放?
(3)在(2)中算出的最小值高度处由静止释放A,经一段时间A 与C 相碰,设碰撞时间极短,碰后一起压缩弹簧,弹簧最大压缩量为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
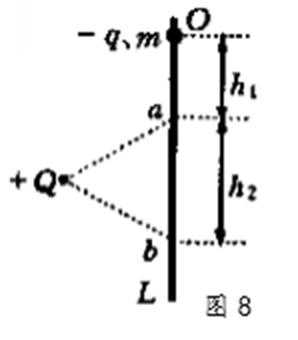
10.如图8所示,L为竖直、固定的光滑绝缘杆,杆上O点套有一质量为m、带电量为-q的小环,在杆的左侧固定一电荷量为+Q的点电荷,杆上a、b两点到+Q的距离相等,Oa之间距离为h1,ab之间距离为h2,使小环从图示位置的O点由静止释放后,小环通过a的速率为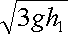
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.某学校兴趣小组对一辆玩具遥控小车的性能进行研究:首先让小车在水平的地面上沿直线运动,记录下小车运动全过程,然后通过对测得的数据进行处理得到如图13所示的v -t图象。已知遥控小车在0~2s内做匀加速直线运动,2s~10s内小车牵引力的功率保持不变,在10s末停止遥控让小车自由滑行。若小车质量m=1kg,设整个过程中小车受到的阻力大小不变.求:
(1)小车在0~2s 和10s~13s的加速度?
(2)在2s~10s内小车牵引力的功率?
(3)小车在加速运动过程中的总位移?
正确答案
(1)根据
(2)小车的匀速运动阶段即7s~10s内,设牵引力为F,则F=f 
且P=

∴P=12 W ⑤
(3)小车的加速运动过程可以分为0~2 s和2 s~7 s两段,设对应的位移分别为


在2 s~7 s内由动能定理可得

解得

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析