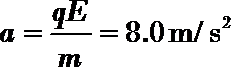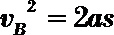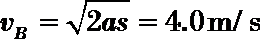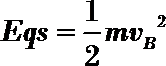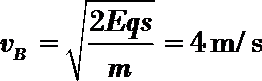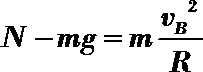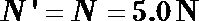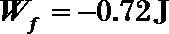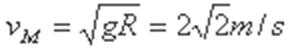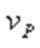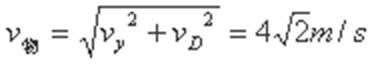- 机械能
- 共1183题
开学初,小源到建设银行营业网点兑换了此前在网上预约的中国高铁纪念币。这枚纪念币由中国人民银行发行,面额10元,每人限兑20枚,且需要提前预约。小源打算与班上同学分享自己的喜悦。他可以向大家这样介绍
①纪念币面额和实际购买力都是由中国人民银行规定的
②纪念币可以直接购买商品,也具有支付手段等货币职能
③纪念币发行量有限,具有一定的收藏价值和升值空间
④纪念币不能与同面额人民币等值流通,必须在规定时间地点使用
正确答案
解析
①错误,国家无权规定纪念币的实际购买力;④错误,纪念币与同面额人民币等值流通,在任何时间地点都可使用;由中国人民银行发行的纪念币属于法定货币,可以直接购买商品,也具有支付手段等货币职能,因其发行量有限,具有一定的收藏价值和升值空间,故②③正确。
知识点
水平地面上有质量分别为m和4m的物A和B,两者与地面的动摩擦因数均为μ。细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示。初始时,绳出于水平拉直状态。若物块Z在水平向右的恒力F作用下向右移动了距离s,重力加速度大小为g。求
17.物块B客服摩擦力所做的功;
18.物块A、B的加速度大小。
正确答案
物块A移动了距离s,则物块B移动的距离为

物块B受到的摩擦力大小为

物块B克服摩擦力所做的功为

解析
A移动了距离s与物块B移动的距离关系,物块B克服摩擦力所做的功
考查方向
解题思路
找到位移关系计算摩擦力做功情况
易错点
位移关系
正确答案
设物块A、B的加速度大小分别为aA、aB,绳中的张力为T。有牛顿第二定律得


由A和B的位移关系得

联立④⑤⑥式得


评分参考:第(1)问3分,①②③式各1分;第(2)问6分,④⑤式各1分,⑥式2分,⑦⑧式各1分。
解析
牛顿第二定律和A和B的位移关系解
考查方向
解题思路
牛顿第二定律和A和B的位移关系解
易错点
合力的计算
19.如图所示,质量为m的小球B,用长为


求:
(1)A球下滑到最低点与B球相碰之前瞬间速度v的大小;
(2)A球与B球撞后粘合在一起瞬间速度v共的大小;
(3)A球与B球撞后的瞬间受到细绳拉力F的大小。
正确答案
解:(1)由机械能守恒:
(2)AB小球组成的系统动量守恒:
(3)以A、B为研究对象:
解析
解析已在路上飞奔,马上就到!
知识点
15.如图竖直放置的光滑1/4圆形轨道PQ,右侧连接一足够长的粗糙平面QB,左侧连接一光滑水平长轨道AP。一条不可伸长的柔软细绳,通过定滑轮将质量M的小球和质量m的滑块连接起来,初始位置M在圆形轨道最低点P,m到Q的距离S=1.2m。已知:M=4kg,m=2kg,R=1m,m和QB平面间的动摩擦因数为=
(1)现对m施加一水平向右的拉力F,将M缓慢拉至Q点,求拉力F所做的功W;
(2)在此位置撤掉拉力F,当M由静止开始从Q点滑至轨道最低点P时,求m的速度v;
(3)通过计算判定:最终m是否和滑轮相撞。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
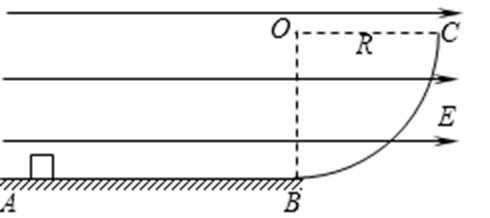
23.如图所示,绝缘光滑水平轨道AB的B端与处于竖直平面内的四分之一圆弧形粗糙绝缘轨道BC平滑连接,圆弧的半径R=0.40m。在轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104N/C。现有一质量m=0.10kg的带电体(可视为质点)放在水平轨道上与B端距离s=1.0m的位置,由于受到电场力的作用带电体由静止开始运动,当运动到圆弧形轨道的C端时,速度恰好为零。已知带电体所带电荷量q=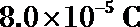
(1)带电体运动到圆弧形轨道的B端时对圆弧轨道的压力;
(2)带电体沿圆弧形轨道从B端运动到C端的过程中,摩擦力做的功。
正确答案
解:(1)设带电体在水平轨道上运动的加速度大小为a,根据牛顿第二定律有
qE =ma
解得
设带电体运动到B端的速度大小为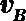
解得
(另解:由
解得
设带电体运动到圆轨道B端时受轨道的支持力为N,根据牛顿第二定律有
解得
根据牛顿第三定律可知,带电体对圆弧轨道B端的压力大小
方向:竖直向下
(2)因电场力做功与路径无关,所以带电体沿圆弧形轨道运动过程中,电场力所做的功
设带电体沿圆弧形轨道运动过程中摩擦力所做的功为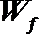
解得
解析
解析已在路上飞奔,马上就到!
知识点
10.水平地面上有两个固定的、高度相同的粗糙斜面甲和乙,乙的斜面倾角大,甲、乙斜面长分别为s、L1,如图所示。两个完全相同的小滑块A、B可视为质点,同时由静止开始从甲、乙两个斜面的顶端释放,小滑块A一直沿斜面甲滑到底端C,而小滑块B滑到底端P后沿水平面滑行到D处(小滑块B在P点从斜面滑到水平面的速度大小不变),在水平面上滑行的距离PD=L2,且s=L1+L2。小滑块A、B与两个斜面和水平面间的动摩擦因数相同,则( )
正确答案
解析
本题有多个选项符合题意,全部选对的得5分,选对但不全的得3分,错选或不答得0分。
知识点
12. 



(3) 若在aO之间距O点x处静止释放该粒子,粒子在磁场区域中共偏转n次到达P点,求x满足的条件及n的可能取值。
正确答案
见解析
解析
解:(1)由题意可知aO=L,粒子在aO加速过程有动能定理:
得粒子经过O点时速度大小:
(2)粒子在磁场区域III中的运动轨迹如图,设粒子轨迹圆半径为R0,
由几何关系可得:
由洛伦兹力公式和牛顿第二定律得:
联立②③④式,得:
(3)若粒子在磁场中一共经过n次偏转到达P,设粒子轨迹圆半径为R,由几何关系有:
依题意有
联立③⑥⑦得
设粒子在磁场中的运动速率为v,有:
在电场中的加速过程,由动能定理: 
联立⑤⑥⑨⑩式,得:
考查方向
本题主要考查带电粒子在磁场中的运动
解题思路

易错点
带电粒子在磁场中的运动的轨迹
知识点
水平地面上有质量分别为m和4m的物A和B,两者与地面的动摩擦因数均为μ。细绳的一端固定,另一端跨过轻质动滑轮与A相连,动滑轮与B相连,如图所示。初始时,绳出于水平拉直状态。若物块Z在水平向右的恒力F作用下向右移动了距离s,重力加速度大小为g。求
17.物块B客服摩擦力所做的功;
18.物块A、B的加速度大小。
正确答案
物块A移动了距离s,则物块B移动的距离为

物块B受到的摩擦力大小为

物块B克服摩擦力所做的功为

解析
A移动了距离s与物块B移动的距离关系,物块B克服摩擦力所做的功
考查方向
解题思路
找到位移关系计算摩擦力做功情况
易错点
位移关系
正确答案
设物块A、B的加速度大小分别为aA、aB,绳中的张力为T。有牛顿第二定律得


由A和B的位移关系得

联立④⑤⑥式得


评分参考:第(1)问3分,①②③式各1分;第(2)问6分,④⑤式各1分,⑥式2分,⑦⑧式各1分。
解析
牛顿第二定律和A和B的位移关系解
考查方向
解题思路
牛顿第二定律和A和B的位移关系解
易错点
合力的计算
24、如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量m1=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后其位移与时间的关系为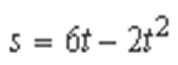
正确答案
见解析
解析
解:
(1)
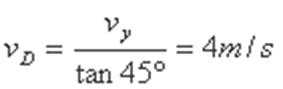
(2)若物块能过最高点,其在M点的速度至少为
设物块在P点的速度至少为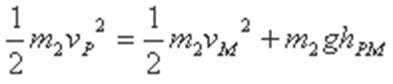
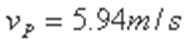
在P点时物块的速度
因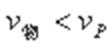
(3)设弹簧长为AC时的弹性势能为EP,物块与桌面间的动摩擦因数为μ 释放m1时,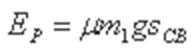
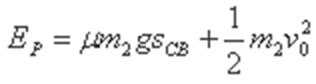
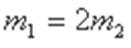
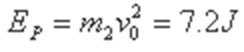
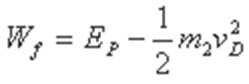
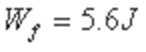
考查方向
本题主要考查平抛运动,圆周运动,机械能守恒,动能定理
解题思路
分析物体不同阶段对应的运动过程,利用相应的规律求解
易错点
摩擦力做功的问题
知识点
16.如图,水平传送带始终保持着大小为V1=2m/s的速度水平向右运动,一质量为m=1kg的物体以V2=4m/s的速度沿传送带水平向左由B向A处运动,已知物体与传送带间的摩擦因数μ=0.2,A、B两点间距离S=6m,从木块放上传送带的B点开始到木块离开传送带为止,(g=10m/s2)试求:
(1)物体在传送带上运动的时间?(2)传送带对物块做功为多大?
正确答案
(1)物体在传送带上运动的时间为4.5s.(2)传送带对物块做功为-6J
解析
(1)物体相对地向左运动的过程,根据牛顿第二定律得:
加速度大小为 a=μmg /m=μg=0.2×10=2m/s2,
设经过时间t1速度减为零,则由0=v2-at1得 t1= v2 /a=4/2s=2s,这段时间内的位移x1=v2/2 t1=4/2×2m=4m;
再设物体向右运动经过时间t2速度与传送带相等,则v1=at2,得t2= v1/a=2/2s=1s这段时间内的位移x2=
(2)向左运动过程,根据动能定理得:传送带对物块做功为W1=0-

考查方向
本题主要考查牛顿第二定律;匀变速直线运动的位移与时间的关系;功的计算
解题思路
(1)物体先向左做匀减速运动,速度减为零后向右做匀加速运动,速度与传送带速度相等后匀速,根据运动学公式,可求出运动的总时间.(2)根据动能定理求解传送带对物块做功.
易错点
对于传送带问题,通常运动分两个过程,要对这两个过程分别进行运动分析和受力分析,然后结合牛顿第二定律和运动学公式求解
知识点
扫码查看完整答案与解析