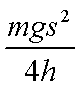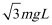- 机械能
- 共1183题
3．下列关于功和机械能的说法，正确的是（ ）
正确答案
解析
（在每小题给出的四个选项中，有一个选项或多个选项正确。全部选对的得3分，选不全的得2分，有选错或不答的得0分）
知识点
9.质量不同的P、Q两球均处于静止状态（如图），敲击弹性金属片，使P球沿水平方向抛出，Q球同时被松开而自由下落．则下列说法中正确的是（ ）
正确答案
解析
AC、根据装置图可知，两球由相同高度同时运动，P做平抛运动，Q做自由落体运动，P在竖直方向上的运动规律与Q相同，则两球同时落地，故AC错误；
B、落地时，P在竖直方向上分速度与Q相同，但是P有水平分速度，所以两球落地时速度大小不同，P球的速度大，但因质量的不同，因此落地时的动能可能相等，故B正确；
D、根据重力做功等于重力势能的变化，虽高度相等，但因质量的不同，则重力势能的变化也不相等，故D错误．
考查方向
研究平抛物体的运动
解题思路
平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，抓住P在竖直方向上的运动规律与Q的运动规律相同，结合等时性分析，并依据重力势能的变化等于重力做功，进行解答.
易错点
关键理解重力势能的变化与重力做功的关系.
知识点
一水平放置的轻弹簧，一端固定，另一端与一小滑块接触，但不粘连；初始时滑块静止于水平气垫导轨上的O点，如图（a）所示，现利用此装置探究弹簧的弹性势能Ep与期其被压缩时长度的改变量x的关系，先推动小滑块压缩弹簧，用米尺测出x的数值；然后将小滑块从天静止释放。用计时器测出小滑块从O点运动至气垫导轨上另一固定点A所用的时间t。多次改变x，测得的x值及其对应的t值如下表所示。(表中的l/t值是根据t值计算得出的)。
（1）根据表中数据，在图(b)中的方格纸上作图线。
（2）回答下列问题：(不要求写出计算或推导过程)
①已知点（0，0）在(1/t)-x图线上，从(1/t)-x图线看， 1/t与x是什么关系？
②从理论上分析，小滑块刚脱离弹簧时的动能Ek与1/t是什么关系(不考虑摩擦力)
③当弹簧长度改变量为x时，弹性势能Ep与相应的Ek是什么关系?
④综合考虑以上分析，Ep与x是什么关系?
正确答案
见解析。
解析
（1）如图。
（2）①图线为经坐标原点的直线，因此
②OA距离
③弹簧与滑块系统机械能守恒，因此
④由于
知识点
7．一质量为m的物体被人用手由静止竖直向上以加速度
A提升过程中，手对物体做功m(
B提升过程中，重力对物体做功m
C提升过程中，物体的重力势能增加m(
D提升过程中，物体重力做功m
正确答案
解析
质量为m的物体被人用手由静止竖直向上以加速度a匀加速提升，由牛顿第二定律可得：F-mg=ma，所以：F=mg+maA、物体匀加速提升h，手对物体做功：W1=Fh=（mg+ma）h．故A正确；
B、D、物体上升h，物体克服重力做功：W=mgh．故BD错误．；
C、提升过程中物体的动能增加量等于物体克服重力做功：W=mgh．故C错误。
考查方向
解题思路
恒力做功，根据W=FS计算
易错点
属于简单题，不应该出错
知识点
7．如图所示，一半径为R，粗糙程度处处相同的半圆形轨道竖直固定放置,直径POQ水平。轨道上的A点离PQ的距离为
Av1 ＜
Bv1 ＞
C从N到Q的过程中，动能与势能相等的点在A点上方，从Q到N的过程中，动能与势能相等的点在A点下方
D从N到Q的过程中，动能与势能相等的点在A点下方，从Q到N的过程中，动能与势能相等的点在A点上方
正确答案
解析
从Q到N摩擦力做功为WQN由动能定理得：mgR-WQN=0,即WQN= mgR，又因为速度减小摩减小，所以
AB、P到N点：mgR-WPN=1/2mv12-Ekp,即
CD、在N点有
故选BC
考查方向
解题思路
因为是曲线运动，所以应该根据动能定理结合牛顿第二定律分析
易错点
在N点有
知识点
如图所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连. 弹簧处于自然长度时物块位于O点(图中未标出). 物块的质量为m,AB =a,物块与桌面间的动摩擦因数为
A物块在A点时,弹簧的弹性势能等于
B物块在B点时,弹簧的弹性势能小于
C经O点时,物块的动能小于
D物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能
正确答案
解析
借助弹簧振子的平衡位置的思想，假定AB的中点为C，则因为物体从A到B想做运动的过程中，摩擦力一直做负功，则过O点弹簧的压缩量一直小于OA，即O点在C的左侧，OA>OB，且OA>
知识点
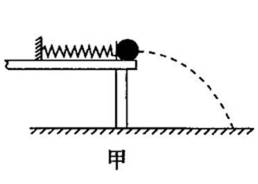
某同学利用下述装置对轻质弹簧的弹性势能进行探究，一轻质弹簧放置在光滑水平桌面上，弹簧左端固定，右端与一小球接触而不固连:弹簧处于原长时，小球恰好在桌面边缘，如图(甲)所示。向左推小球，使弹簧压缩一段距离后由静止释放:小球离开桌面后落到水平地面。通过测量和计算，可求得弹簧被压缩后的弹性势能。
回答下列问题：
（1）本实验中可认为，弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等。已知重力加速度大小为g。为求得Ek，至少需要测量下列物理量中的 （填正确答案标号）。
a.小球的质量m
b.小球抛出点到落地点的水平距离s
c.桌面到地面的高度h
d.弹簧的压缩量△x
e.弹簧原长L0
（2）用所选取的测量量和已知量表示Ek，得Ek= 。
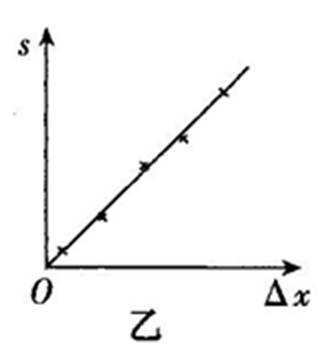
（3）图（乙）中的直线是实验测量得到的s-△x图线。从理论上可推出，如果h不变.m增加，s—△x图线的斜率会（填“增大”、“减小”或“不变”）；如果m不变，h增加，s—△x图线的斜率会（填“增大”、“减小”或“不变”）。由图（b）中给出的直线关系和Ek的表达式可知，Ep与△x的 次方成正比。
正确答案
答案：(1)abc
(2)
（3）减小 增大 2
解析
（2）由（1）问所述可知
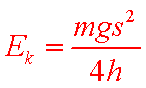
（3）
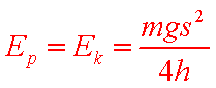
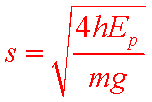
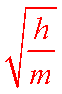
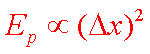
知识点
蹦床比赛分成预备运动和比赛动作。最初，运动员静止站在蹦床上在预备运动阶段，他经过若干次蹦跳，逐渐增加上升高度，最终达到完成比赛动作所需的高度；此后，进入比赛动作阶段。
把蹦床简化为一个竖直放置的轻弹簧，弹力大小F=kx (x为床面下沉的距离，k为常量)。质量m=50kg的运动员静止站在蹦床上，床面下沉x0=0.10m；在预备运动中，家丁运动员所做的总共W全部用于其机械能；在比赛动作中，把该运动员视作质点，其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s，设运动员每次落下使床面压缩的最大深度均为xl。取重力加速度g=I0m/s2，忽略空气阻力的影响。
（1）求常量k，并在图中画出弹力F随x变化的示意图；
（2）求在比赛动作中，运动员离开床面后上升的最大高度hm;
（3）借助F-x 图像可以确定弹性做功的规律，在此基础上，求 x1 和W的值
正确答案
答案：见解析
解析
（1）床面下沉
有
F-x图线如图所示。
（2）运动员从x=0处离开床面，开始腾空，由运动的对称性知其上升、下落的时间相等，
（3）参照由速度时间图线求位移的方法可知F-x图线下的面积等于弹力做的功，从x处到x=0处，弹力做的功
运动员从
对整个预备运动过程分析，由题设条件以及功和能的关系，有
解得W=2525J.
知识点
5.如图所示，固定的竖直光滑长杆上套有质量为m的小圆环，圆环与水平状态的轻质弹簧一端连接，弹簧的另一端连接在墙上，并且处于原长状态，现让圆环由静止开始下滑，已知弹簧原长为L，圆环下滑到最大距离时弹簧的长度变为2L（未超过弹性限度），则在圆环下滑到最大距离的过程中（ ）
A圆环的机械能守恒
B弹簧弹性势能变化了
C圆环下滑到最大距离时，所受合力为零
D圆环重力势能与弹簧弹性势能之和保持不变
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
23.如图所示，弹簧的一端固定，另一端连接一个物块，弹簧质量不计。物块（可视为质点）的质量为 m，在水平桌面上沿 x 轴运动，与桌面间的动摩擦因数为 µ。以弹簧原长时物块的位置为坐标原点 O，当弹簧的伸长量为 x 时，物块所受弹簧 弹力大小为 F=kx,k 为常量。
（1）请画出 F 随 x 变化的示意图；并根据 F-x 的图像求物块沿 x 轴从 O 点运动到位置 x 的 过程中弹力所做的功。
a. 求弹力所做的功.并据此求弹性势能的变化量；
b. 求滑动摩擦力所做的功；并与弹力做功比较，说明为什么不存在与摩擦力对应的“摩擦力势能”的概念。
正确答案
（1）
（2）
因为摩擦力做功与路程成正比，而非像弹簧弹力做功一样与路径无关，只与初末位置有关，所以无“摩擦势能”的概念。
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析