- 正弦函数的奇偶性
- 共48题
设









正确答案
解析
识别条件:偶函数,偶函数说明啥?定义:f(-x)=f(x)恒成立!还有图像关于y轴对称!
这就是转化一念间 对任意的

周期函数为4 在



设
知识点
在复平面内,复数
正确答案
解析
略
知识点
设数列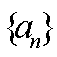
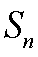
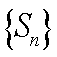
则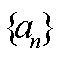
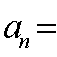
正确答案
解析
识别条件:数列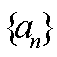
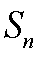
继续识别条件:数列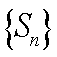
继续识别条件:数列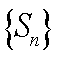
an=S1 n=1
知识点
定义在

① 


② 
③ 


(1)求函数
(2)设



正确答案
见解析。
解析
(1)
∵ 


∴

由

又



代入(



(2)由已知得:若存在



设
则
令


当



当



∴

又


于是有
知识点
15.在锐角


(Ⅰ)求
(Ⅱ)若

正确答案
(Ⅰ)由正弦定理可得
因为
所以
在锐角

(Ⅱ)由余弦定理可得
又因为
所以
解得
经检验,由
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析