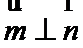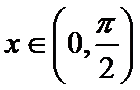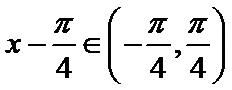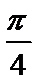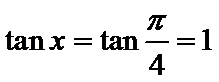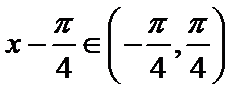- 正弦函数的奇偶性
- 共48题
1
题型:简答题
|
请考生从2题中选做一题
14.(坐标系与参数方程选做题)已知直线





15.(几何证明选讲选作题)如图1,已知












第(1)小题正确答案及相关解析
正确答案

解析
依题已知直线








考查方向
本题考查极坐标与平面直角坐标的互化、点与直线的距离,属于基础题.
解题思路
先将直线
易错点
极坐标与平面直角坐标的互化。
第(2)小题正确答案及相关解析
正确答案

解析
如下图所示,连接












考查方向
本题考查直线与圆、直角三角形的射影定理,属于中档题.
解题思路
连接OC,则易得

易错点
图形中几何关系的寻找,射影定理的应用。
1
题型:
单选题
|
8.





结论正确的是( )
正确答案
D
解析
如图,
由题意,












考查方向
1.平面向量的线性运算;2.平面向量的数量积.
解题思路
先根据向量相关性质把有向线段用坐标的形式表示出来,然后利用垂直关系求得。
易错点
计算错误,向量的数量积表示错误
知识点
正弦函数的奇偶性
1
题型:简答题
|
在平面直角坐标系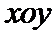
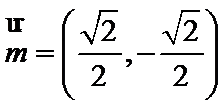
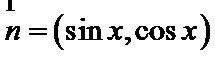
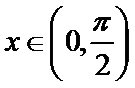
16.若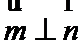
17.(2)若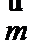
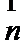
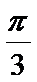
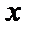
第(1)小题正确答案及相关解析
正确答案
(1)
解析
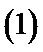
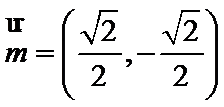
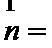
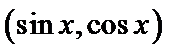
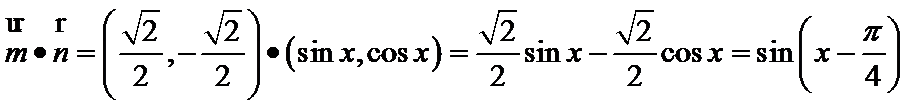

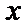

考查方向
本题考查向量的垂直,向量数量积的坐标运算,向量的夹角公式以及三角函数的运算,属于中档题.
解题思路
第一问,由两向量垂直,利用数量积等于零,结合坐标运算,可以得出正切值。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
第(2)小题正确答案及相关解析
正确答案
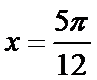
解析
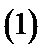
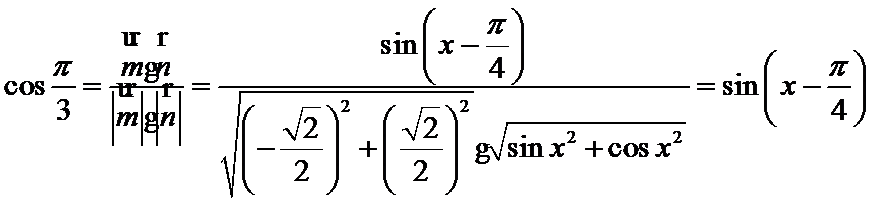

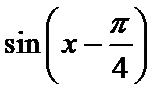
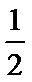

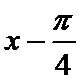
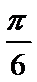

考查方向
本题考查向量的垂直,向量数量积的坐标运算,向量的夹角公式以及三角函数的运算,属于中档题.
解题思路
第二问,结合向量的夹角公式,列出方程求解即可。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
下一知识点 : 正弦函数的定义域和值域
扫码查看完整答案与解析