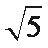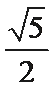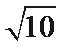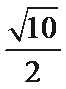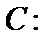- 双曲线的定义及标准方程
- 共193题
7.设双曲线

正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
11.设点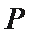
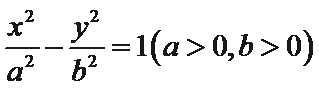
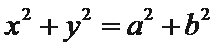
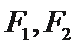
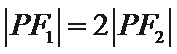
正确答案
解析
根据题意易知圆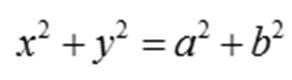
由此可知三角形为直角三角形,因此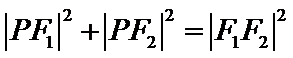
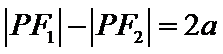
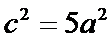
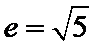
考查方向
解题思路
画出草图,结合图形通过题目条件确定a与c的代数关系,即可求出双曲线的离心率。
易错点
本题容易因为对双曲线的定义不会应用而导致题目不会做。
知识点
11. 已知双曲线
正确答案
解析
如下图所示,在三角形OF2B1中,由面积相等可得






考查方向
解题思路
根据题中条件建立等式,进而求出双曲线的离心率。
易错点
对于已知条件不知如何处理导致出错。
知识点
12.已知双曲线






正确答案
解析
双曲线


故双曲线


所以双曲线

知识点
如图,
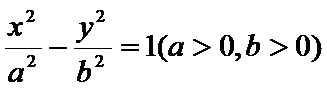
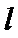
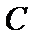
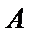
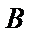
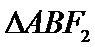
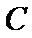
正确答案
解析
因为A、B是双曲线上的点
所以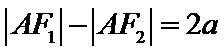
因为是等边三角形,
所以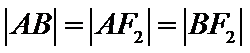
所以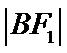
所以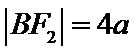
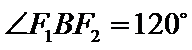
所以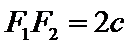
所以根据余弦定理,
可得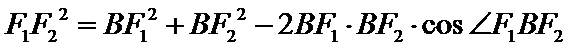
将数据代入得,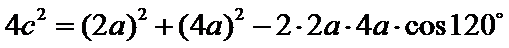
整理得,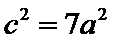
所以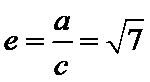
所以选B
考查方向
解题思路
利用双曲线的性质,结合余弦定理求解
易错点
计算能力,想不到利用余弦定理
知识点
10.已知正实数m,n满足:m+n=1,且使



正确答案
解析
由:m+n=1知





考查方向
解题思路
先由均值不等式求出m的值,再求
易错点
均值不等式不会用导致出错。
知识点
7.已知双曲线


正确答案
解析
c2=5+m=9,解得m=4=b2,所以
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
本题考查双曲线的焦点位置及渐近线方程,解题步骤如下:
1、由题可知,易得x2的系数为负,y2系数为正。
2、c2=5+m=9,解得m=4.
易错点
本题易在求解时把分母平方运算。
知识点
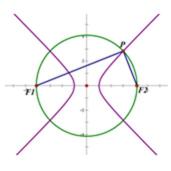
7.如图,已知











正确答案
解析
由
可得PF1=F1F2=2C,
由于

所以QF2
所以:
由双曲线的定义:QF1-QF2=2
所以选择答案A
考查方向
解题思路
根据几何性质,找到几何关系,从而利用三角形的性质解决。
易错点
容易将P点看成是双曲线上的点,从而得到:2c=3a。
知识点
7.已知双曲线

正确答案
解析
易知,抛物线焦点坐标为




考查方向
本题主要考查了求双曲线的标准方程,在近几年的各省高考题出现的频率较高,常与椭圆、抛物线等知识点交汇命题。
解题思路
先求出抛物线的焦点坐标,即求出此b,再根据c2=a2+b2即可求出双曲线的标准方程。
易错点
抛物线与双曲线定义不清楚导致出错。
知识点
3.“

正确答案
解析
由题可知,当m>3时,方程我双曲线方程,反之不成立。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查双曲线和简易逻辑
解题思路
按照双曲线的标准方程求解B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断条件时发生错误。
知识点
扫码查看完整答案与解析