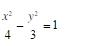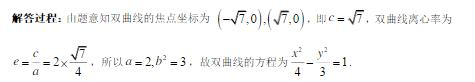双曲线的几何性质
共199题

· 双曲线的几何性质

双曲线的几何性质
共199题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

若实数满足，则的最小值为.

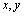
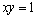
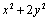
正确答案

解析

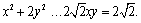
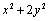
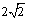
由基本不等式可得故的最小值为.

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

已知双曲线：的离心率为2.若抛物线的焦点到双曲线的渐近线的距离为2，则抛物线的方程为

正确答案

解析

抛物线的焦点，双曲线的渐近线为，不妨取，即，焦点到渐近线的距离为，即，所以双曲线的离心率为，所以，所以，所以抛物线方程为，选D.

知识点

双曲线的几何性质抛物线的标准方程和几何性质

题型：填空题

填空题 · 4 分

已知双曲线的一条渐近线的方程为，则。

正确答案

解析

由得渐近线的方程为即，由一条渐近线的方程为得2。

知识点

双曲线的几何性质

题型：填空题

填空题 · 5 分

已知双曲线C1：(a＞0，b＞0)与双曲线C2：有相同的渐近线，且C1的右焦点为F(，0)，则a＝__________，b＝__________。

正确答案

1;2

解析

∵C1与C2的渐近线相同，∴。

又C1的右焦点为F(，0)，∴，即a2＋b2＝5。

∴a2＝1，b2＝4，∴a＝1，b＝2

知识点

双曲线的几何性质

题型：简答题

简答题 · 13 分

已知三点O(0,0)，A(－2,1)，B(2,1)，曲线C上任意一点M(x，y)满足.

(1)求曲线C的方程；

(2)点Q(x0，y0)(－2＜x0＜2)是曲线C上的动点，曲线C在点Q处的切线为l，点P的坐标是(0，－1)，l与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比。

正确答案

(1) x2＝4y； (2)2

解析

(1)由＝(－2－x,1－y)，＝(2－x,1－y)，

得，

＝(x，y)·(0,2)＝2y，

由已知得，

化简得曲线C的方程：x2＝4y.

(2)直线PA，PB的方程分别是y＝－x－1，y＝x－1，曲线C在Q处的切线l的方程是，且与y轴的交点为F(0，)，

分别联立方程组解得D，E的横坐标分别是，，

则xE－xD＝2，|FP|＝1－，

故S△PDE＝|FP|·|xE－xD|＝，而，

则，即△QAB与△PDE的面积之比为2

知识点

双曲线的几何性质

题型：填空题

填空题 · 5 分

若双曲线的离心率e=2，则m=____.

正确答案

解析

根据双曲线方程：知，，并在双曲线中有：，离心率e==2=,

m=48

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

设a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，则过A（a，a2），B（b，b2）两点的直线与双曲线﹣=1的公共点的个数为（　　）

正确答案

解析

∵a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，

∴a+b=﹣，ab=0，

过A（a，a2），B（b，b2）两点的直线为y﹣a2=（x﹣a），即y=（b+a）x﹣ab，

即y=﹣x，

∵双曲线﹣=1的一条渐近线方程为y=﹣x，

∴过A（a，a2），B（b，b2）两点的直线与双曲线﹣=1的公共点的个数为0。

知识点

双曲线的几何性质直线与双曲线的位置关系

题型：填空题

填空题 · 4 分

已知双曲线和椭圆有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 .

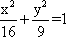
正确答案

解析

知识点

椭圆的几何性质双曲线的定义及标准方程双曲线的几何性质

题型：单选题

单选题 · 5 分

已知双曲线的左顶点与抛物线的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的准线的交点坐标为（-2，-1），则双曲线的焦距为（）

正确答案

解析

双曲线的渐近线为，由双曲线的一条渐近线与抛物线的准线的交点坐标为（－2，－1）得，即，

又∵，∴，将（－2，－1）代入得，

∴，即

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

若，则的定义域为（）

正确答案

解析

知识点

双曲线的几何性质

继续学习学习下一知识点

下一知识点 : 双曲线的相关应用

百度题库 > 高考 > 文科数学 > 双曲线的几何性质

扫码查看完整答案与解析