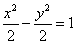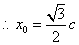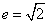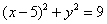- 双曲线的定义及标准方程
- 共193题
给出以下命题:
① 双曲线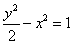
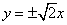
② 命题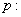
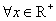
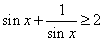
③ 已知线性回归方程为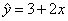
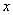
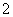
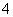
④ 已知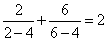
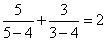
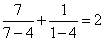
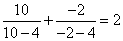
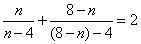
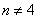
则正确命题的序号为 (写出所有正确命题的序号)。
正确答案
①③④
解析
略
知识点
若双曲线

正确答案
解析
略
知识点
已知双曲线

正确答案
解析
略
知识点
曲线
(1)若曲线

(2)若曲线


(3)设
















正确答案
见解析
解析
(1)由题意知:
解得:
(2)化简得:
由题意得:
解得:
(3)直线代入椭圆方程得:


由韦达定理得:

设




=
将①②代入上式得:
故


知识点
已知双曲线

正确答案
解析
略
知识点
过点(2,3)且以
正确答案
解析
略
知识点
已知双曲线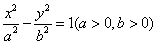
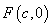
(1)若双曲线的一条渐近线方程为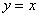
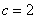
(2)以原点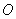
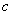
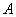
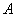
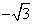
正确答案
见解析。
解析
解:(1)
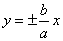
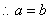
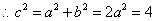
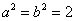

(2)设点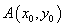

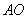
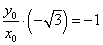
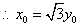
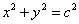

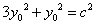
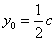
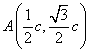
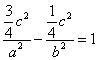
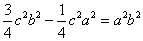
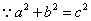

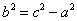
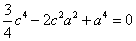
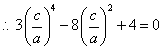
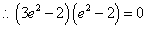
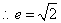
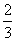
知识点
过双曲线
正确答案
解析
略
知识点
等轴双曲线







正确答案
解析
略
知识点
以双曲线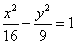
正确答案
解析
略
知识点
扫码查看完整答案与解析