- 直线与抛物线的位置关系
- 共49题
在平面直角坐标系中,





(1)求曲线
(2)若过点




(3)若曲线




正确答案
见解析
解析
(1)依题意知,动点




以原点为顶点,
∵
∴
∴ 曲线

(2)当




此时
当


则由
设


∴

(3)设
∴
∵
∴
∵
∴
当且仅当 
∵
∴当

知识点
已知抛物线














(1)求证:

(2)若











正确答案
见解析
解析
解析:(1)设


所以



所以







(2)设

由
同理
所以面积
设

由


得到

②得

所以当


所以当




所以

知识点
设点P是曲线C:x2=2py(p>0)上的动点,点P到点(0,1)的距离和它到焦点F的距离之和的最小值为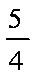
(1)求曲线C的方程;
(2)若点P的横坐标为1,过P作斜率为k(k≠0)的直线交C于点Q,交x轴于点M,过点Q且与PQ垂直的直线与C交于另一点N,问是否存在实数k,使得直线MN与曲线C相切?若存在,求出k的值;若不存在,请说明理由。
正确答案
见解析。
解析
(1)依题意知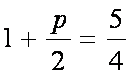
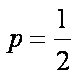
所以曲线
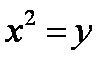
(2)由题意直线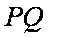
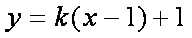
联立方程组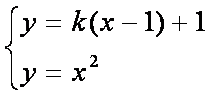
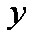
得
所以得直线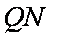
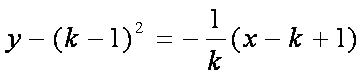
代入曲线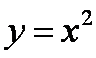
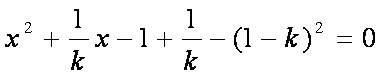
解得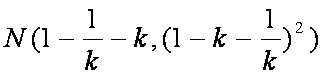
所以直线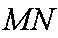
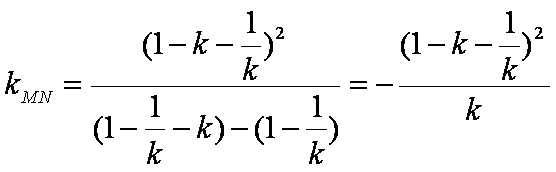
过点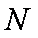
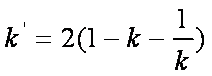
由题意有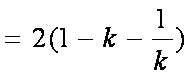
解得
故存在实数
知识点
“a=2”是“直线y=﹣ax+2与y=
正确答案
解析
解:当a=2时直线y=﹣ax+2的斜率是﹣2,直线y=
满足k1•k2=﹣1
∴a=2时直线y=﹣ax+2与y=
直线y=﹣ax+2与y=

“a=2”是“直线y=﹣ax+2与y=
故选A。
知识点
在平面直角坐标系xOy中,已知直线l的参数方程为


正确答案
见解析。
解析
直线l:

∴交点

知识点
扫码查看完整答案与解析