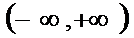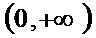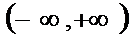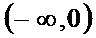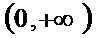- 导数的应用
- 共1166题
4.若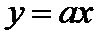
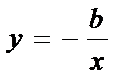
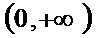
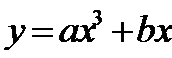
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数
(I)当


(II)在区间



正确答案
(I)当


曲线


所以曲线


(II)解1:
当




故



当

若

若

所以

因此有

解得
这与
当




所以



综上所述,

解2:有已知得:
设







解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(I)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(II)当a≠0时,求函数f(x)的单调区间与极值。
正确答案
(I)解:当a=1时,
又
所以,曲线y=f(x)在点(2,f(2))处的切线方程为
即6x+25y﹣32=0.
(II)解:

由于a≠0,以下分两种情况讨论.
(1)当a>0时,令f'(x)=0,得到
当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)在区间
在区间
函数f(x)在


函数f(x)在x2=a处取得极大值f(a),且f(a)=1.
(2)当a<0时,令f'(x)=0,得到
当x变化时,f'(x),f(x)的变化情况如下表:
所以f(x)在区间(﹣∞,a)

函数f(x)在x1=a处取得极大值f(a),且f(a)=1.
函数f(x)在


解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数f(x)=x2+mx+ln x是单调递增函数,则m的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知

(1)当


(2)求

正确答案
(1)当


所以

即曲线



所以曲线


即
(2)因为

令

①若




②若




当



所以当


③若




所以当


综上可知,当


当



当



解析
解析已在路上飞奔,马上就到!
知识点
20.设
(1)若


(2)若


正确答案
(1)-5
(2)
解析
解析已在路上飞奔,马上就到!
知识点
16.若函数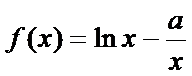
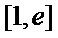
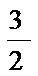
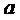
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知

(1)

(2)是否存在实数


(3)在(1)的条件下,求证:
正确答案
(1)
减区间
极小值
(2)










所以存在
(3)



而
解析
解析已在路上飞奔,马上就到!
知识点
10.已知可导函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.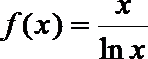
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析