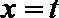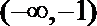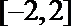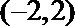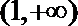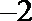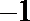- 导数的应用
- 共1166题
20.设

(1)若

(2)若函数



(3)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数
(1)当
(2)若函数
(3)若对于任意的

正确答案
解:(1)
当
令
当

所以
在区间
(2)

则方程

这时,
因此满足条件的
(3)由(2)知,当
当
因此函数
又
于是
因此满足条件的
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)讨论
(Ⅱ)若

(Ⅲ)设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数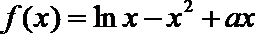
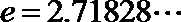
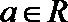
(Ⅰ)当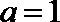
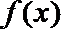
(Ⅱ)若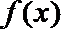
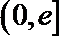
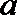
(Ⅲ)设函数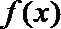
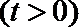
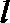
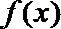
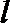
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数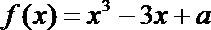
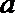
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率p与日产量x(单位:件,x∈N*)间的关系为
(I)将日利润y(元)表示成日产量x(件)的函数;
(II)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在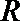
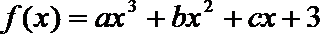
① 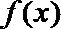
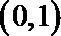
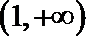
② 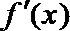
③ 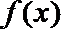
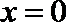
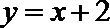
(1)求函数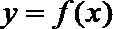
(2)设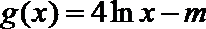
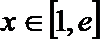
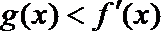
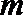
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设曲线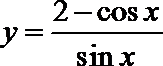
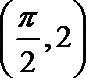
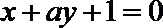
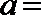
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析