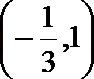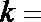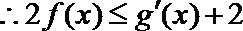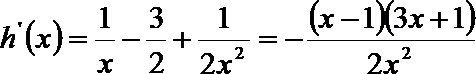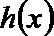- 导数的应用
- 共1166题
21.已知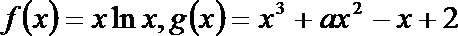
(I)如果函数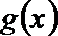
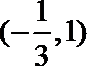
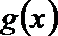
(II)在(Ⅰ)的条件下,求函数y=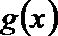
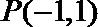
(III)若不等式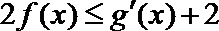
正确答案
解: (I)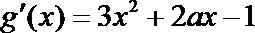
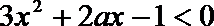
即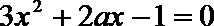
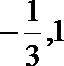
将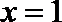
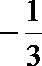
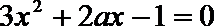
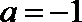
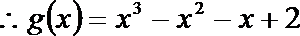
(II)由(Ⅰ)知: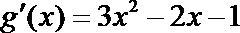
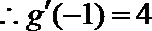
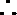
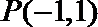
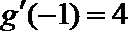
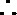
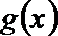
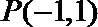
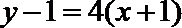
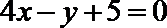
(III)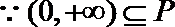
即: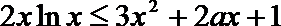
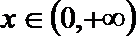
可得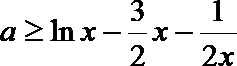
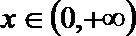
设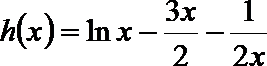
令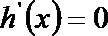
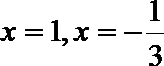
当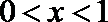
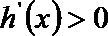
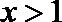
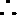
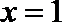
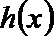
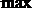
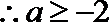
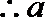
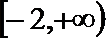
解析
解析已在路上飞奔,马上就到!
知识点
21.函数


(Ⅰ)求
(Ⅱ)解关于

正确答案
解:
(Ⅰ)
由函数在

∴

∴
∴
(Ⅱ)
∵对应方程的根为
∵
∴解集为
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数f(x)=x2-x+alnx
(1)当


(2)讨论
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)当

(2)设|MN|=

(3)在(2)的条件下,若对任意的正整数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若函数
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(1)设


(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知

(1)当

(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在R上定义运算*:a*b=2ab+2a+b,且f(x)= 
正确答案
解析
知识点
2.已知定义域为R的函数f(x)满足f(x)=2x+ax(a>0且a≠1),且f(x)的导函数满足f'(x)>2,则a的取值范围为( )
正确答案
解析
由f'(x)>2可知f'(x)-2>0,设F(x)=f(x)-2x,∴F'(x)>0,∴F(x)是R上的单调递增函数.又由f(x)=2x+ax可知f(x)-2x=ax,故a>1.
知识点
6.设f=3x-3-x+x3,若当t>0时,f(m+3t)+f(mt-t2)≤0恒成立,则实数m的取值范围是( )
正确答案
解析
由题意知函数f是定义在R上的奇函数且为增函数,故f(m+3t)≤f(t2-mt),m+3t≤t2-mt对任意的t>0恒成立,即m≤


知识点
扫码查看完整答案与解析