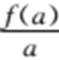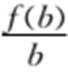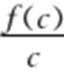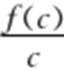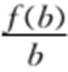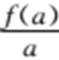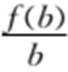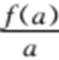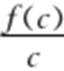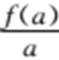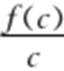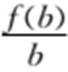导数的应用_章节学习

1

题型：填空题

|

填空题 · 5 分

16.若函数f(x)=的定义域为R，则实数m的取值范围为。

正确答案

(－1，+∞)

解析

由m≠x－ex，设g(x)=x－ex，得g'(x)=1－ex，显然x<0时，g'(x)>0，此时函数g(x)递增；

x>0时，g'(x)<0，此时函数g(x)递减；

于是当x=0时，函数有最大值g(0)=－1，于是函数g(x)的值域为(－∞，－1].

欲使x∈R时，都有m≠x－ex，则m的取值范围为(－1，+∞).

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围

1

题型：单选题

|

单选题 · 5 分

10.在R上定义运算*:a*b=2ab+2a+b,且f(x)= 则不等式f(x)<-1的解集为（）

A( ,1)

B(-1, )∪(1,+∞)

C(- , )∪(1,+∞)

D(-1,2)

正确答案

C

解析

知识点

利用导数研究函数的单调性利用导数求函数的最值

1

题型：单选题

|

单选题 · 5 分

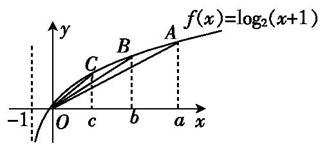
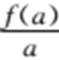
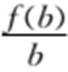
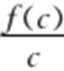
2.已知f(x)=log2(x+1)，且a>b>c>0，则，，的大小关系是（）

A>>

B>>

C>>

D>>

正确答案

B

解析

如图，

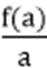
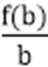
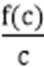
易知kOA=<kOB=<kOC=.

知识点

利用导数研究函数的单调性

1

题型：单选题

|

单选题 · 5 分

12.已知函数，若存在唯一的零点，则的取值范围是（）

A ；

B ；

C ；

D [

正确答案

D

解析

在上要恒成立，所以，故选D。

考查方向

本题主要考查函数的导数与单调性的关系以及零点问题。

解题思路

根据函数的导函数恒大于等于零最后转化为求函数的最值问题。

易错点

1、不能通过函数的导函数来解决问题。

知识点

导数的运算利用导数研究函数的单调性

1

题型：简答题

|

简答题 · 12 分

21.已知函数f(x)= -ln x(a0). （1）求函数f(x)的单调区间；（2）当a = l时，求f(x)在区间[,2]上的最大值和最小值(0.69<ln 2<0.70)；（3）求证ln ≤

正确答案

1）函数的定义域为，

若，

故，函数在区间上单调递减，

时，在区间上单调递增，在上单调递减所以单调递减区间为

（2）时，，

由（1）可知，在上单调递增，在区间[1,2]上单调递减，

所以在区间上的最大值为而

故函数在区间上的最小值为

（3）由（2）可知，函数在区间（0,1）上单调递增，

故有

解析

f(x)求导并整理，得到f(x)在x>0区间上单调递减，然后分类讨论a的不同取值对单调区间的影响。利用函数单调性证明不等式恒成立的条件。

考查方向

本题主要考查函数的单调性和函数的最值。

解题思路

本利用导数求单调区间，利用函数与不等式关系求最大值最小值

易错点

不会利用导数求函数单调区间。

知识点

利用导数研究函数的单调性利用导数求函数的最值利用导数证明不等式

1

题型：简答题

|

简答题 · 14 分

20．已知函数，其中为常数

（1）根据的不同取值，判断函数的奇偶性，并说明理由；

（2）若，判断函数在上的单调性，并说明理由.

正确答案

(1)既不是奇函数也不是偶函数

(2)单调递增

解析

(1)的定义域为关于原点对称.

,

当时,故为奇函数.

当时，由,知

且,

故既不是奇函数也不是偶函数.

(2)设,则

,

由得

,,

,又,

所以

得

从而,即.

故当时,在上单调递增.

知识点

函数奇偶性的判断利用导数研究函数的单调性

1

题型：单选题

|

单选题 · 5 分

5．已知函数f（x）＝－cosx，则f（x）在[0，2π]上的零点个数为

A1

B2

C3

D4

正确答案

C

解析

由图可知，2个函数图像有3个交点。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查函数图像及零点

解题思路

1、分别画出2个函数图像；

2、求出交点个数，即可得到结果。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易在画图时发生错误。

知识点

函数零点的判断和求解利用导数研究函数的单调性利用导数求函数的极值

1

题型：单选题

|

单选题 · 5 分

10．已知函数f（x）＝x＋，g（x）＝＋a，若∈[，3]，∈[2，3]，使得f（x1）≥g（x2），则实数a的取值范围是

Aa≤1

Ba≥1

Ca≤0

Da≥0

正确答案

A

解析

f（x）min=f（1）=5, g（x）min = g（2）=4+a,得a≤1。B选项不正确，C选项不正确，D选项不正确，所以选A选项。

考查方向

本题主要考查函数的值域

解题思路

1、求出f(x)在[，1]上的最小值，g(x)在[2,3]上的最小值；

2、求出f（x）min≥g（x）min，即可得到结果。B选项不正确，C选项不正确，D选项不正确，所以选A选项。

易错点

本题易在判断范围大小时发生错误。

知识点

利用导数研究函数的单调性不等式恒成立问题

1

题型：简答题

|

简答题 · 12 分

21．设函数f（x）＝－mlnx，g（x）＝－(m＋1)x，m＞0．

（Ⅰ）求函数f（x）的单调区间；

（Ⅱ）当m≥1时，讨论函数f（x）与g（x）图象的交点个数．

正确答案

（1）当时，函数的单调增区间是，无减区间；当时，函数的单调增区间是，减区间是；（2）一个．

解析

（1）直接按照步骤来求；

（2）要注意对参数的讨论．

⑴解：函数的定义域为，，

当时，，所以函数的单调增区间是，无减区间；

当时，；当时，，函数的单调递减；

当时，，函数的单调递增.

综上：当时，函数的单调增区间是，无减区间；当时，函数的单调增区间是，减区间是.

⑵解：令，问题等价于求函数的零点个数，

当时，，有唯一零点；

当时，，

当时，，函数为减函数，注意到，，所以有唯一零点；

当时，或时，时，所以函数在和单调递减，在单调递增，注意到，，所以有唯一零点；

当时，或时，时，所以函数在和单调递减，在单调递增，意到，所以，而，所以有唯一零点.

综上，函数有唯一零点，即两函数图象总有一个交点.

考查方向

本题考查了利用导数求含参数的函数极值，分类讨论，讨论点大体可以分成以下几类：

1、根据判别式讨论；

2、根据二次函数的根的大小；

3、定义域由限制时，根据定义域的隐含条件；

4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论；

5、多次求导求解等．

解题思路

1、求导，然后解导数不等式，求单调区间。

2、对参数分类讨论得结论。

易错点

第二问中的易丢对a的分类讨论。

知识点

函数零点的判断和求解利用导数研究函数的单调性

1

题型：单选题

|

单选题 · 5 分

12. 若函数的导函数在区间（1，2）上有零点，则在下列区间上单调递增的是（）

A

B

C

D

正确答案

D

解析

因为，

所以，

另，

所以，

所以可得的单调增区间为，，

所以结合选项，b的取值范围为，选择D

考查方向

函数的单调性与单调区间，导数与函数的单调性

解题思路

先根据导函数在区间上有零点，得到b的取值范围，再利用b的取值范围，求出函数的单调区间，结合题目，选择正确的选项

易错点

判断b的取值范围，

知识点

函数零点的判断和求解导数的运算利用导数研究函数的单调性

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点