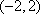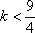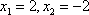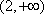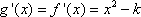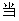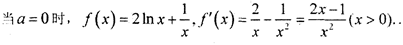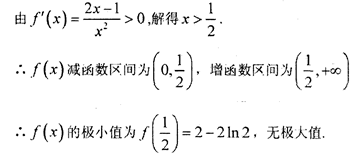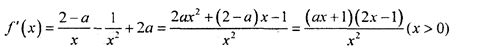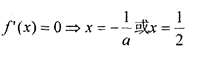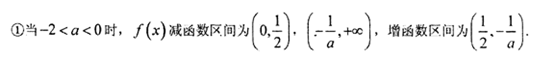- 导数的应用
- 共1166题
已知函数
(1)求a的值;
(2)是否存在实数b,使得函数
正确答案
见解析。
解析
(1)由函数




(2)函数


故存在实数:
知识点
已知函数

(1)当


(2)讨论
正确答案
见解析
解析
(1)当


所以

因此,



又



即
(2)

(i)当
因为



(ii)当
因为



(iii)当




所以


综上,当


当


在
知识点
函数
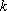
(1) 当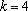
(2) 若曲线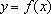
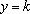
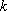
正确答案
(1)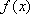
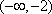
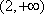
(2)
解析
(1)因为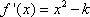
当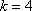
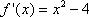
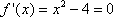
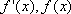

………………4分
所以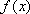
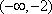
单调递减区间是
(2)令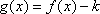
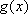
因为
当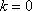
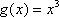
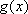
当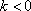
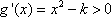
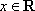
所以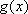
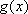
当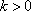
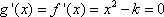
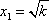
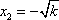
所以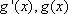

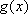
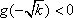
即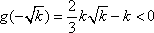
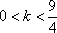
综上所述,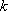
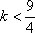
知识点
已知函数
(1)求
(2)当

正确答案
见解析
解析
(1) 定义域为

令



--------------------------------5分
所以


(2) 证明1:
设




所以


所以,当

所以

所以,当

证明2:
令

令



---------------------10分


当

故
即当

知识点
已知函数

(1)讨论函数
(2)若函数




正确答案
见解析
解析
(1)在区间

①若



②若


在区间


在区间


综上所述,①当


②当



(2)因为函数

解得
由已知

令

易得


所以

知识点
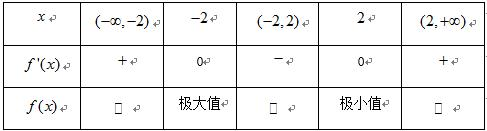
函数f (x)的定义域为R,导函数
正确答案
解析
由题图知
知识点
已知函数

(1)求函数g(x)的单调区间;
(2)若函数f(x)在(1,+∞)上是减函数,求实数a的最小值;
(3)当a≥



正确答案
见解析。
解析
知识点
已知函数


(1)求实数
(2)设
①若


②是否存在点



正确答案
见解析
解析
(1)








(2)①



在
令

设






②由


表明:若点


而线段



这也表明存在点


则这两个封闭图形面积相等, ————13分
知识点
已知函数
(1) 求函数
(2) 证明:对任意的


(3) 设(2)中所确定的




正确答案
见解析。
解析
(1)解:函数


当


所以函数

(2)证明:当


由(1)知

故存在唯一的

(3)证明:∵


∴
其中,


当



所以


∴当

知识点
已知函数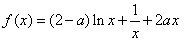
(1)当
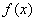
(2)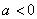
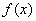
(3)若对任意的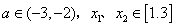
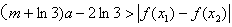
正确答案
见解析。
解析
(1)解:
(2)
知识点
扫码查看完整答案与解析