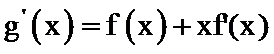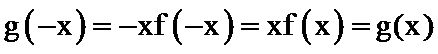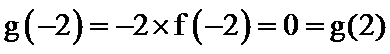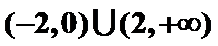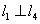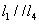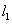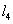- 导数的应用
- 共1166题
已知函数
26.若函数


27.若斜率为






正确答案

解析



因为函数




解得
考查方向
解题思路
直接求导,


易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
正确答案
证明略
解析
设点



要证
即证










即

考查方向
解题思路
设出交点坐标,用分析法证明,要证



易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
已知函数
26.若函数


27.若斜率为






正确答案

解析



因为函数




解得
考查方向
解题思路
直接求导,


易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
正确答案
证明略
解析
设点



要证
即证










即

考查方向
解题思路
设出交点坐标,用分析法证明,要证



易错点
函数的恒成立问题,构造新函数;用导数解决函数的综合性问题
12.设函数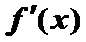
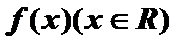
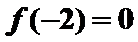
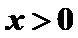
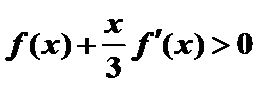
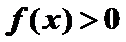
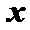
正确答案
解析
设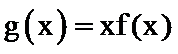
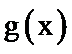
∵当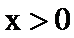
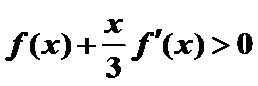
即当时,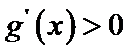
∴当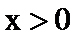
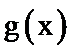
又∵
∴函数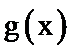
∴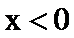
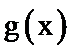
又∵
∴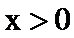
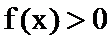
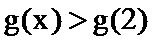
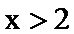
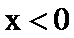
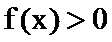
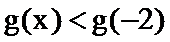
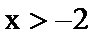
∴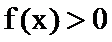
故选B.
考查方向
解题思路
构造函数g(x),利用g(x)的导数判断函数g(x)的单调性与奇偶性,求出不等式的解集即可.
易错点
本题的难点和易错点在于函数g(x)的构造.
知识点
21.已知函数f(x)=(x -2)ex+a(x -1)2.
(Ⅰ)讨论f(x)的单调性; (Ⅱ)若有两个零点,求a的取值范围.
正确答案
1
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若空间中四条两两不相同的直线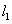
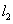
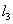
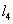


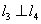
正确答案
解析
略
知识点
21. 设函数
(1)讨论

(2)证明:当

正确答案
(1)

当

当





当b满足0<b<




(2)由(1),可设




当

故





由于

故当

解析
解析已在路上飞奔,马上就到!
知识点
8. 对于R上可导的任意函数f(x),若满足
正确答案
解析
由








两式相加得
考查方向
解题思路
有已知不等式,分类讨论得到函数的单调性,求出最小值
易错点
不会利用已知不等式得到函数的单调性。
知识点
已知函数
25.若函数





26.若



正确答案

解析
已知函数

又函数








令
所以函数的单调递减区间为
考查方向
解题思路
利用切线与已知直线垂直可得两直线的斜率相等。再利用导数的几何意义,函数在某一点的导数,为该点的切线的斜率。得到一个关于a,b的等式。再由函数在x=1处取得极值点,得到x=1处的导函数为零,联立方程组可得,a,b的值;最后求出导函数得到单间区间。
易错点
熟悉导数的几何意义,以及用等式研究函数的单调性。
正确答案
解析
当





即


考查方向
解题思路
由函数在区间





易错点
熟悉恒成立问题的求解方法。
扫码查看完整答案与解析