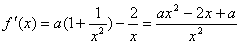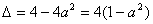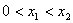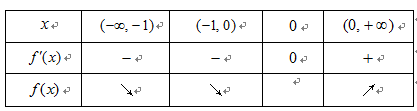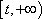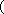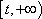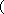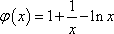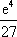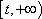- 导数的应用
- 共1166题
已知

正确答案
解析
略
知识点
已知函数
(1) 求f(x)的反函数的图象上图象上点(1,0)处的切线方程;
(2)证明: 曲线y = f (x) 与曲线
(3)设a<b, 比较

正确答案
见解析
解析
(1) f (x)的反函数


(2) 证明曲线y=f(x)与曲线
因此,
所以,曲线y=f(x)与曲线
(3)设
令


所以
知识点
设函数
(1)若函数
(2)当a=1时,求函数
正确答案
见解析。
解析
(1)∵
∴
令
当x变化时,

故函数
因此



解得

(2)当a=1时,


①当t+3<-1,即t<-4时,
因为


②当

因为





由





③当t+3>2,即t>-1时,
由②得







综上所述,当a=1时,


知识点
已知函数


(1)如果函数


(2)设



(3)记函数


正确答案
见解析。
解析
(1)

令




∴



(2)假设存在,即存在

当

















(3)据题意有

5个实根两两不相等。
(ⅰ)

(ⅱ)
















因为(ⅰ)(ⅱ)要同时满足,故

下证:这5个实根两两不相等,即证:不存在


时成立.
若存在

由


当

当

又由


而当

同的零点,故舍去,所以这5个实根两两不相等。
综上,当

知识点
已知函数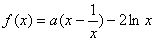
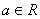
(1)若a=1,判断函数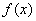
(2)求函数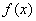
(3)设函数
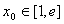
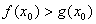
正确答案
见解析。
解析
(1)当
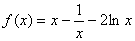
因为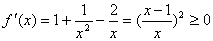
所以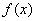
所以函数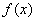
(2)函数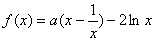
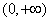
当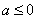
因为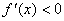
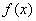
当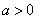
当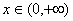
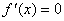
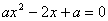
①当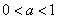
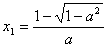
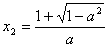
因为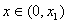
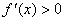
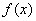
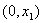
因为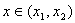
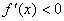
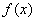
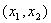
因为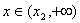
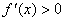
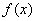
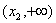
②当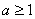
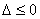
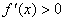
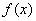
综上,当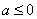
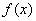
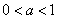
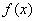
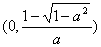
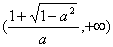
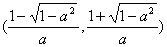
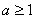
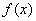
(3)由存在一个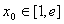
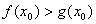
得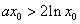

令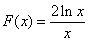
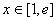
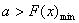
因为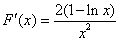
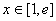
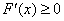
所以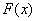
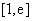
故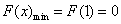
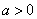
知识点
已知函数f(x)=x2e-x.
(1)求f(x)的极小值和极大值;
(2)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围。
正确答案
(1)极小值为f(0)=0;极大值为f(2)=4e-2.
(2)(-∞,0)∪[
解析
(1)f(x)的定义域为(-∞,+∞),
f′(x)=-e-xx(x-2),①
当x∈(-∞,0)或x∈(2,+∞)时,f′(x)<0;
当x∈(0,2)时,f′(x)>0.
所以f(x)在(-∞,0),(2,+∞)单调递减,在(0,2)单调递增。
故当x=0时,f(x)取得极小值,极小值为f(0)=0;
当x=2时,f(x)取得极大值,极大值为f(2)=4e-2.
(2)设切点为(t,f(t)),
则l的方程为y=f′(t)(x-t)+f(t)。
所以l在x轴上的截距为m(t)=
由已知和①得t∈(-∞,0)∪(2,+∞)。
令h(x)=

当x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3)。
所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[
综上,l在x轴上的截距的取值范围是(-∞,0)∪[
知识点
已知函数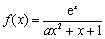
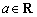
(1)若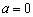
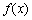
(2)当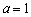
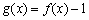
正确答案
见解析
解析
(1)解:函数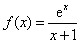
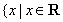
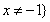
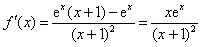
令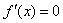
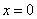
当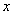

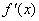
……………… 4分
故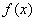
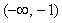
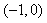
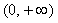
所以当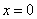
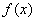
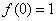
(2)解:结论:函数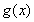
证明过程如下:
由题意,函数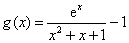
因为 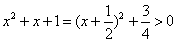
所以函数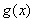
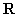
求导,得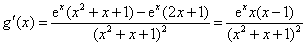
令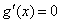
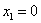
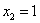
当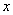
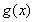
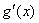
故函数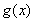
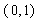
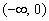
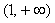
当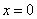
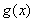
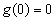
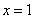
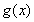
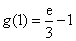
因为函数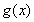
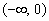
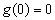
所以对于任意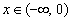
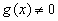
因为函数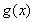
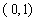
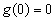
所以对于任意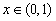
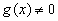
因为函数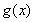
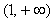
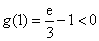
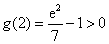
所以函数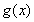
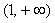
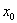
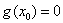
故函数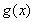
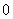
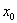
知识点
函数
正确答案
7
解析
略
知识点
已知函数

(1)当

(2)若对



正确答案
见解析。
解析
(1)当


令

当


当

当


∴当

当

(2)∵


即

①当

即

∵

∴
②当

即

∵

∴
知识点
已知函数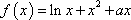
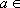
(1)若函数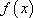

(2)当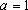

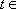
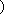

值。
( 参考数值: 自然对数的底数
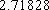
正确答案
见解析。
解析
(1)解法1:函数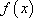
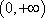
∵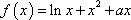
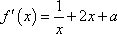
∵ 函数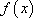
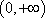
∴ 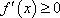
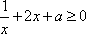
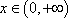
∴ 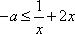
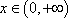
当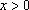
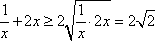
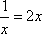
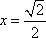
∴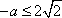
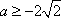
∴
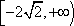
解法2:函数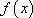
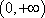
∵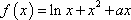
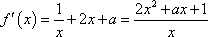
方程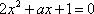
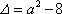
① 当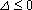
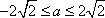
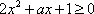
此时, 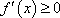
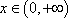
故函数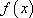
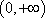
② 当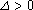
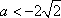
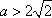
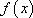
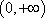
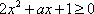
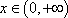
设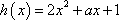
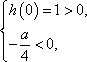
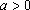
故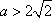
综合①②得
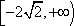
(2)解:当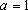
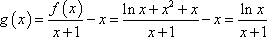
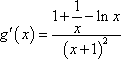
∵ 函数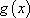
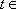
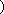
∴ 方程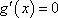
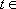
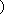
即方程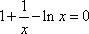
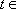
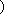
令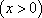
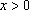
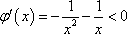
∴函数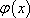
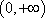
∵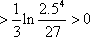
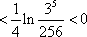
∴函数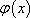
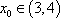
∵方程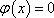
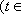
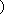
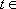
∴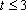
∵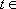

∴

知识点
扫码查看完整答案与解析