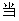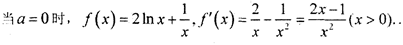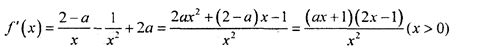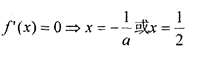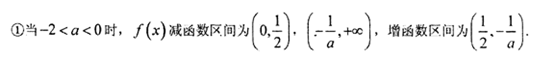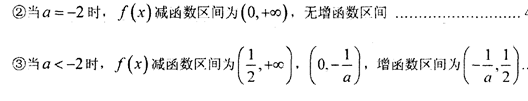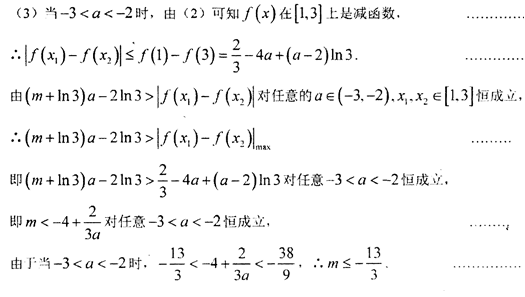- 导数的应用
- 共1166题
从一堆苹果中任取10只,称得它们的质量如下(单位:克):
则样本数据落在[114.5,124.5)内的频率为( )
正确答案
解析
从所给的10个数据可以看出120、122、116、120这四个数字落在[114.5,124.5)内,所以数据落在[114.5,124.5)内的频率为=0.4.故选C.
知识点
如图,





正确答案
解析
略
知识点
某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.根据经验知道,若每台机器产生的次品数P(万件)与每台机器的日产量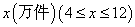
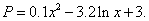
(1)试将该工厂每天生产这种元件所获得的利润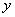
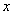
(2)当每台机器的日产量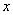
正确答案
见解析。
解析
知识点
已知函数
(1)若函数
(2)若函数
(3)若

正确答案
见解析。
解析
知识点
如图是甲,乙两名同学
正确答案
87;甲
解析
略
知识点
已知函数

(1)讨论函数
(2)若函数




正确答案
见解析
解析
(1)在区间

①若



②若


在区间


在区间


综上所述,①当


②当



(2)因为函数

解得
由已知

令

易得


所以

知识点
函数f (x)的定义域为R,导函数
正确答案
解析
由题图知
知识点
函数
正确答案
解析
略
知识点
已知函数





(1)求
(2)若函数

正确答案
见解析。
解析
(1)由





又∵曲线


由<1><2><3>可求得,
(2)若函数




∴方程
解得:

所以当实数


知识点
已知函数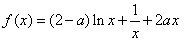
(1)当
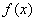
(2)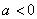
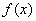
(3)若对任意的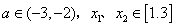
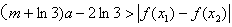
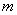
正确答案
见解析。
解析
(1)解:
(2)
知识点
扫码查看完整答案与解析