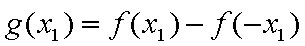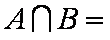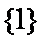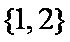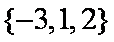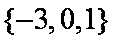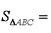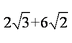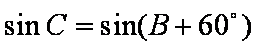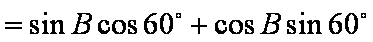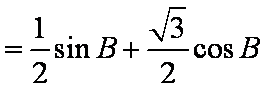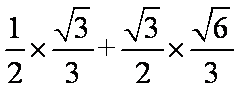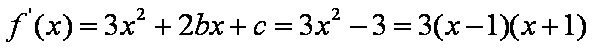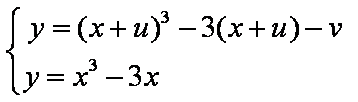- 导数的应用
- 共1166题
已知

(1)求函数
(2)求证:当


正确答案
见解析
解析
解析:(1)


∴当


(2)当


当


设

∵




当



因此当


知识点
已知函数f(x)=(3x2-6X+6)ex-x3
(1)求函数f(x)的单调区间及极值;
(2)若 x1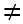
正确答案
见解析。
解析
(1)∵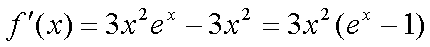
∴当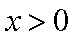
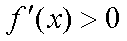
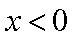
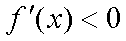
则
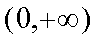
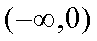
所以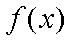
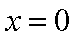
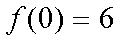
(2)∵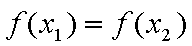
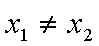
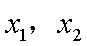
不妨设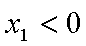

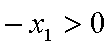
令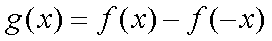
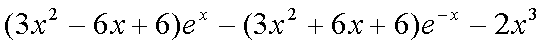
则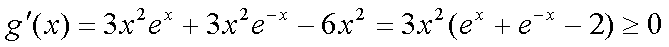
所以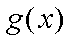
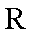
又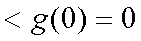
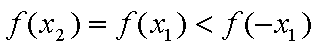
又∵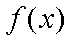
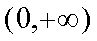
∴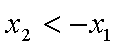

知识点
已知

(1)若


(2)求
(3)设



正确答案
见解析
解析
(1) 


经检验, 
(2) 
(i)当


(ii)当

① 若




② 若



综上所述,当


当



(3)当


易知


注意到
故由题设知

故

知识点
集合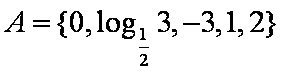

正确答案
解析
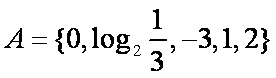
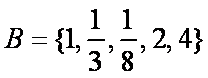
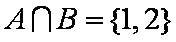
知识点
在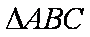
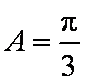
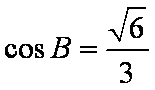
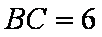
(1)求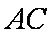
(2)求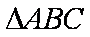
正确答案
(1)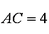
解析
(1)因为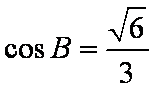

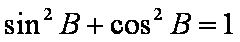
所以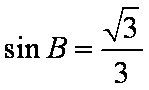
由正弦定理得,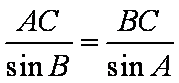
所以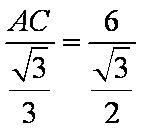
所以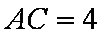
(2)在
=
=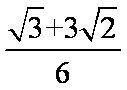
所以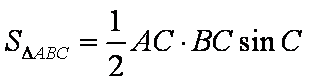
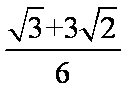
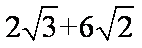
知识点
已知函数

(1)若曲线




(2)在(1)的条件下,证明


(3)若




正确答案
见解析。
解析
(1)

∵曲线


∴ 

(2)设
则
∴当





在
∴


∴

(3)原方程可化为
令



















又



知识点
已知正ΔABC边长为3,












(1)求
(2)求数列
正确答案
见解析。
解析
(1)BPn=an,BPn+1=an+1,则BPn=0.5an,QnC=3-0.5an,CRn=1.5-0.25an,
ARn=1.5+0.25an,APn+1=0.75+0.125an,BPn+1=
(2)由





则
令
所以
知识点
已知平面上的动点


(1)求动点

(2)过点




求直线
(3)试问在曲线





两点,使得

正确答案
见解析。
解析
(1)设

化简得曲线

(2)设

由 

令直线AB方程为
由
则
由 ①和
代入
依题意直线AB的斜率大于0,即 

故直线AB的方程为
(3)设



切线


则切线

由

又


设
得
所以
故存在点

知识点
设函数


正确答案
答案:
解析
略
知识点
已知函数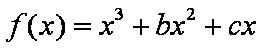
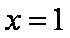
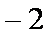
(1)求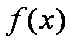
(2)若对任意的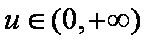
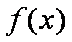
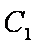

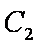
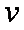
正确答案
(1)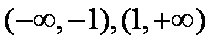
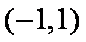
(2)
解析
(1)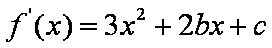
由题意得: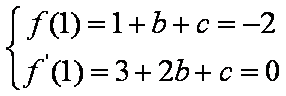
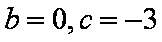
∴
∴当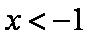
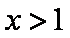

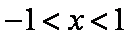
∴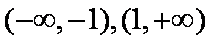
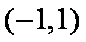
(2)
由方程组
得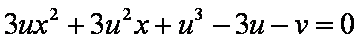
∴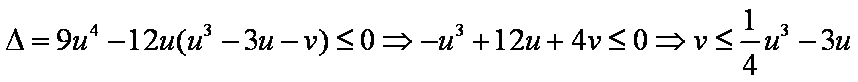
……………………………………9 分
令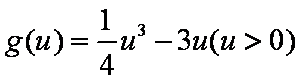
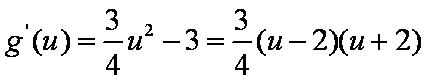
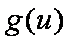
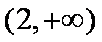
所以当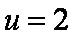
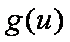
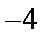
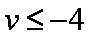
知识点
扫码查看完整答案与解析