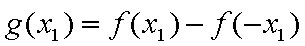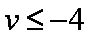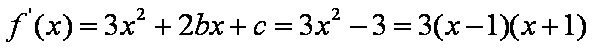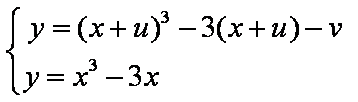- 导数的应用
- 共1166题
已知函数


(1)求

(2)对函数



正确答案
见解析
解析
解析:
(1)由
而点


又直线
故有
(2)由(1)得
由

令
令
故

故当

当
从而当





故
要使



知识点
已知

(1)求函数
(2)求证:当


正确答案
见解析
解析
解析:(1)


∴当


(2)当


当


设

∵




当



因此当


知识点
已知函数f(x)=(3x2-6X+6)ex-x3
(1)求函数f(x)的单调区间及极值;
(2)若 x1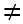
正确答案
见解析。
解析
(1)∵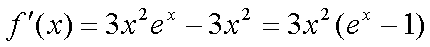
∴当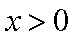
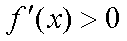
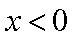
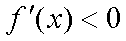
则
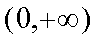
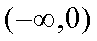
所以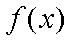
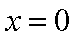
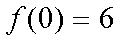
(2)∵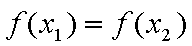
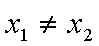
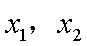
不妨设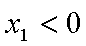

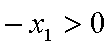
令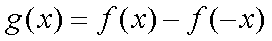
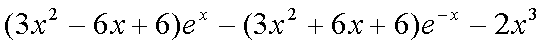
则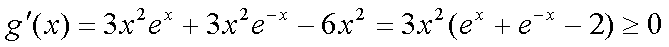
所以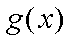
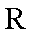
又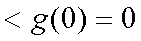
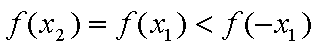
又∵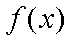
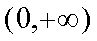
∴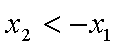

知识点
已知函数
(1)若

(2)若


正确答案
见解析
解析
(1)当













(2)由







令




∴
即


知识点
设二次函数






正确答案
解析
略
知识点
若函数


(1)函数
(2)已知函数


正确答案
见解析
解析
(1)函数
则定义域内存在实数

构造函数

∵



∴

即存在

另解:函数
由

即
作函数

由图象可以看出,存在

即
(2)

由已知,存在

即
整理,得

∴

由


∴a的取值范围是
知识点
已知函数
(1)若函数

(2)若对任意给定的
使得
正确答案
见解析。
解析
(1)因为



令












(2)







当
当







此时,当
又因为,当








令













综合①④可知,当
在

知识点
已知x=1是函数f(x)=mx3﹣3(m+
(1)求m与n的关系表达式;
(2)求f(x)的单调区间;
(3)当x∈[﹣1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
正确答案
见解析。
解析
(1)f′(x)=3mx2﹣6(m+1)x+n。
因为x=1是f(x)的一个极值点,所以f'(1)=0,即3m﹣6(m+1)+n=0。
所以n=3m+6。
(2)由(1)知f′(x)=3mx2﹣6(m+1)x+3m+6=3m(x﹣1)[x﹣(1+
当m<0时,有1>1+
由上表知,当m<0时,f(x)在(﹣∞,1+


(3)由已知,得f′(x)>3m,即3m(x﹣1)[x﹣(1+
∵m<0.∴(x﹣1)[x﹣1(1+
10x=1时,(*)式化为0<1怛成立。
∴m<0。
20x≠1时∵x∈[﹣1,1],∴﹣2≤x﹣1<0。
(*)式化为

令t=x﹣1,则t∈[﹣2,0),记g(t)=t﹣
则g(t)在区间[﹣2,0)是单调增函数,∴g(t)min=g(﹣2)=﹣2﹣

由(*)式恒成立,必有



综上10、20知﹣
知识点
已知函数
(1)若


(2)若

正确答案
(1)
(2)
解析
(1)由


所以

所以所求切线方程为
即
(2)由已知

因为函数

即不等式

令

当


当


由此得


知识点
已知函数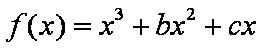
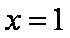
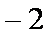
(1)求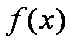
(2)若对任意的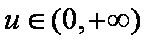
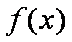
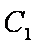

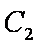
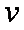
正确答案
(1)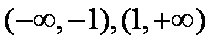
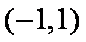
(2)
解析
(1)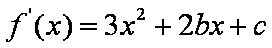
由题意得: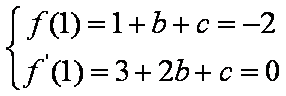
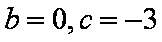
∴
∴当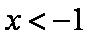
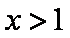

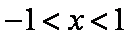
∴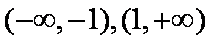
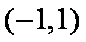
(2)
由方程组
得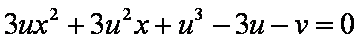
∴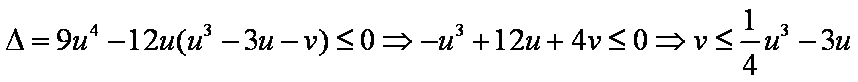
……………………………………9 分
令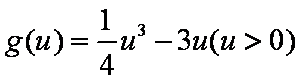
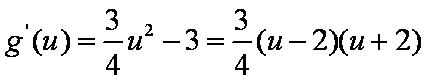
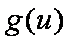
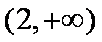
所以当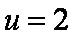
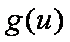
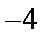
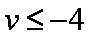
知识点
扫码查看完整答案与解析