- 导数的应用
- 共1166题
已知

(1)若


(2)求
(3)设



正确答案
见解析
解析
(1) 


经检验, 
(2) 
(i)当


(ii)当

① 若




② 若



综上所述,当


当



(3)当


易知


注意到
故由题设知

故

知识点
已知函数

(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)-1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为

正确答案
见解析
解析
(1)
曲线y=f(x)在x=1处的切线为2x-y-2=0,
曲线y=g(x)在x=1处的切线方程为2x-y-1=0. ……………3分
两直线间的距离为
(2)令h(x)=f(x)-g(x)+1, ,则
当a≤0时, 注意到x>0, 所以
又h(1)=0,故0<x<1时,h(x)>0,即f(x)> g(x)-1,与题设矛盾. ……………6分
当a>0时,
当


所以h(x)在上是增函数,在上是减函数, ……………8分
∴h(x)≤
因为h(1)=0,又当a≠2时,≠1,

所以a=2. ……………9分
(3)当a<0时,由(2)知
不妨设0<x1≤x2,则|h(x1)-h(x2)|=h(x1)-h(x2),|x1-x2|=x2-x1, ……………10分
∴|h(x1)-h(x2)|≥|x1-x2
等价于h(x1)-h(x2)≥x2-x1,即h(x1)+x1≥h(x2)+x2, ……………11分
令H(x)=h(x)+x=alnx-x2+x+1,H(x)在(0,+∞)上是减函数,
∵
∴-2x2+x+a≤0在x>0时恒成立,∴a≤(2x2-x)min ……………13分
又x>0时, (2x2-x)min=
∴a≤-,又a<0,∴a的取值范围是
知识点
已知函数

(1)若曲线




(2)在(1)的条件下,证明


(3)若




正确答案
见解析。
解析
(1)

∵曲线


∴ 

(2)设
则
∴当





在
∴


∴

(3)原方程可化为
令



















又



知识点
定义域为R 的连续函数f(x) ,对任意x 都有


正确答案
解析



2<a<4, 

知识点
20. 已知函数




(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(I)求函数
(II)设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数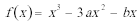
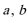
(1)若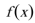
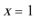
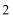
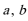
(2)若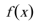
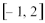
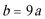
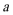
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





























